PolyFit
- Updated2023-02-21
- 3 minute(s) read
Advanced Analysis Library Only
AnalysisLibErrType PolyFit (double arrayX[], double arrayY[], ssize_t numberOfElements, int order, double outputArray[], double coefficients[], double *meanSquaredError);
Purpose
 |
Note This function has been superseded by PolyFitEx. |
Finds the coefficients that best represent the polynomial fit of the data points (X, Y) using the least squares method. PolyFit obtains the ith element of the output array using the following formula:
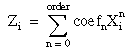
PolyFit obtains the mean squared error (mse) using the following formula:
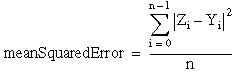
where order is the polynomial order, and numberOfElements is the number of sample points. The size of coefficients must be greater than or equal to order + 1.
PolyFit can perform this operation in place; that is, the input and output arrays can be the same.
If the elements in arrayX are large and order is also large, you might see unstable results. One solution is to scale the input data elements to the range [–1:1]. To do this, perform the following steps:
- Find the number, for example, k, in arrayX that has the largest magnitude, or absolute value.
- Divide all elements in the array by the absolute value of k.
- Apply Polyfit and rescale the results in the output array by multiplying all elements in the output array by the absolute value of k.
Example Code
/* Generate a 10th-order polynomial pattern with random coefficients and find the polynomial fit. */
double x[200], y[200], z[200], a[11], coef[11];
double first, last, mse;
n, k, order;
n = 200;
first = 0.0;
last = 1.99E2;
Ramp (n, first, last, x) /* x[i] = i */
k = 11;
Uniform (k, 17, a);
PolyEv1D (x, n, a, k, y); /* polynomial pattern */
/* Find the best polynomial fit. */
order = 10;
PolyFit (x, y, n, order, z, coef, &mse);
Parameters
| Input | ||
| Name | Type | Description |
| arrayX | double [] | An array whose elements contain the X coordinates of the (X,Y) data sets. |
| arrayY | double [] | An y whose elements contain the Y coordinates of the (X,Y) data sets. |
| numberOfElements | ssize_t | Number of sample points used in the polynomial fit operation. |
| order | int | The order of the polynomial used in the polynomial fit operation. Polynomial order must be greater than or equal to 0. If the polynomial order is less than zero, this function sets the coefficients parameter to an empty array and returns an error. In real applications, polynomial order is less than 10. If the polynomial order is greater than 25, the function sets the coefficients beyond order 25 in the coefficients parameter to zero and returns a warning. |
| Output | ||
| Name | Type | Description |
| outputArray | double [] | The polynomial values that best represent the data. |
| coefficients | double [] | Polynomial coefficients that best describe the polynomial curve fit. The size of coefficients must be greater than or equal to order + 1. |
| meanSquaredError | double | The mean squared error generated by the difference between the fitted curve and the raw data. |
Return Value
| Name | Type | Description |
| status | AnalysisLibErrType | A value that specifies the type of error that occurred. Refer to analysis.h for definitions of these constants. |
Additional Information
Library: Advanced Analysis Library
Include file: analysis.h
LabWindows/CVI compatibility: LabWindows/CVI 3.1 and later
Examples
Refer to the following examples that use the PolyFit function:
- analysis\polyfit1.cws
Open example - apps\freqresp\freqresp.cws
Open example