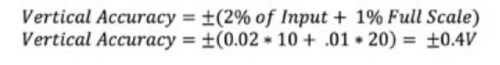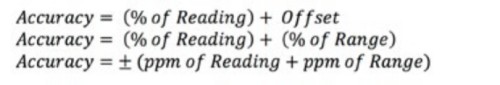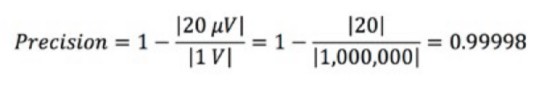模拟采样质量：精度、灵敏度、精确度和噪声。

在参考采样质量时，需评估测量的精度和精确度。但在此之前首先要了解示波器的灵敏度，这一点很重要。灵敏度是输入信号可引起测量设备响应的最小变化。换言之，如果输入信号发生一定程度的改变（达到灵敏度阈值），数字数据就会发生变化。

切勿将灵敏度与分辨率和代码宽度混淆。其中分辨率定义了代码宽度；这是仪器显示值的离散级别。而灵敏度则定义仪器记录值变化所需的电压变化。例如，测量范围为10 V的仪器也许能够以1 mV分辨率检测信号，但它可以测量的最小可检测电压可能为15 mV。这种情况下仪器的分辨率为1 mV，灵敏度为15 mV。

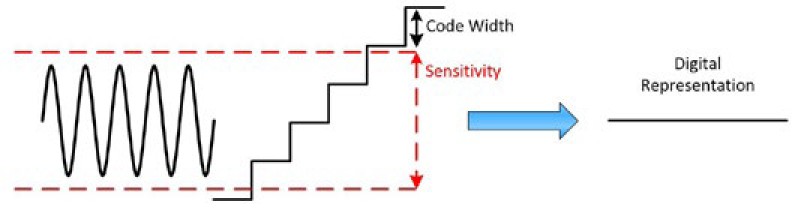
某些情况下灵敏度会大于代码宽度。这似乎不符合常理，难道电压的变化量可显示但无法记录？是的！因此，为充分理解其优势，请设想使用恒定直流电压的情况。尽管电压完全恒定且没有偏差是最理想的情况，但信号总会存在一些细微的变化，如图1所示。灵敏度用红线表示，代码宽度也绘制在图中。本例中的电压永远不会超过灵敏度水平，因此即使大于代码宽度也由相同的数值表示。其优势在于，它不会拾取噪声，并将信号更准确地表示为恒定电压。

^{图1：灵敏度大于代码宽度有助于平滑处理噪声信号。}

在信号实际开始上升至超过灵敏度水平后，信号就会由不同数值表示。请​参见​图2。请记住，测量值的精确性永远不会超过灵敏度。

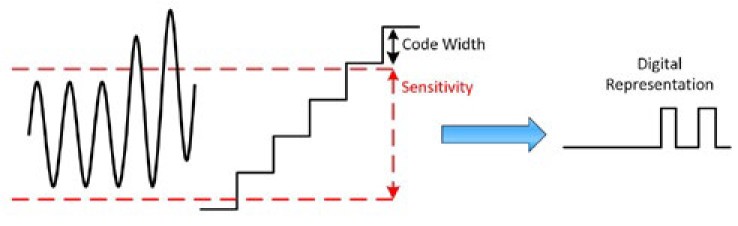
^{图2：信号超过灵敏度水平后，则由不同数值表示。}

仪器灵敏度的定义也存在一些歧义。有时，它可如上所示定义为常量。在这种情况下，信号超过灵敏度水平后，则由不同数值表示。但有时它也会被定义为信号的变化量。当信号变化量超过指定的灵敏度量，就会由不同的信号表示。这种情况下，绝对电压并不重要，重要的是电压变化量。此外，某些仪器将灵敏度定义为约等于零。 

不仅不同公司对灵敏度的确切定义不同，同一家公司不同产品的灵敏度含义也略有不同。查看仪器产品规范以了解其灵敏度定义非常重要；如描述不完整，请联系公司获取相关说明。

精度是一个度量项，反映了仪器如实指示测量信号值的能力。该术语与分辨率无关，但是仪器的精度永远不可能高于分辨率。

不同仪器或数字化仪的精度要求也有所不同。例如，一般来说，数字万用表(DMM)的精度应高于示波器。精度的计算方式也会因设备而异，但请务必查看仪器的产品规范，以了解特定仪器的精度计算方式。 

示波器的精度

示波器分别定义了水平和垂直系统的精度。水平系统是指时间刻度或X轴；水平系统精度是时间基准的精度。垂直系统是指测量电压或Y轴；垂直系统精度是增益和偏移精度。通常，垂直系统精度比水平系统精度更重要。

垂直精度通常表示为输入信号的百分比和满量程的百分比。某些产品规范将输入信号分解为垂直增益和偏移精度。公式1所示为精度的2种不同定义方式。 

^{公式1：计算示波器的垂直精度。}

例如，示波器可通过以下方式定义垂直精度： 

输入信号为10 V，量程为20 V，则可计算精度： 

DMM和电源的精度

DMM和电源通常以读数的百分比指定精度。公式2所示为DMM或电源精度的3种不同表达方式。

^{公式2：计算DMM或电源的垂直精度。}

术语ppm是指百万分之一。大多数产品规范还具有多个用于确定精度的表。精度取决于测量类型、量程和最近一次校准时间。查看产品产品规范，了解如何计算精度。 

例如，DMM设置为10 V量程，校准后90天在23 ℃±5 ℃下工作，预期信号为7 V。产品规范将这些条件下的精度规定为±（读数的20 ppm + 量程的6 ppm）。然后便可计算精度：

此时读数应处于实际输入电压的200μV范围内。  

DAQ设备的精度

DAQ卡通常将精度定义为与理想传递函数的偏差。公式3所示为DAQ卡指定精度方式的示例。

^{公式3：计算DAQ设备的精度。}

然后定义各个术语： 

大多数这些术语均可在表中定义，并以标称范围为基础。规范中还定义了噪声不确定度的计算方式。噪声不确定度是由于测量中噪声的影响而导致的测量不确定度，是确定精度的因素。

此外，设备可能有多个精度表，具体取决于查找目标是模拟输入精度还是模拟输出精度，或是否启用或禁用了滤波器。

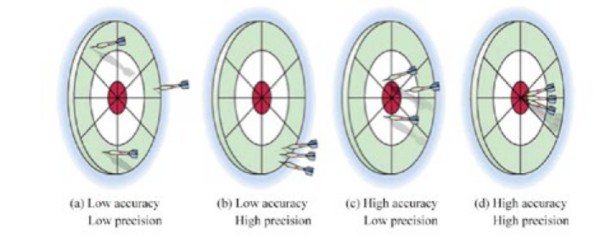
精度和精确度通常可互换使用，但存在细微差别。精确度定义为测量仪器的稳定性及其对同一输入信号反复进行相同测量的能力。精度是指测量值与实际值的接近程度，而精确度指的是重复多次同一测量值之间的一致程度。 

^{图3：精确度和精度相关但不相同。}

仪器的噪声和短期漂移对精确度的影响最大。制造商通常不直接提供仪器的精确度，但可根据其他规范进行推断，如传输比规范、噪声和温度漂移。如果已有一系列测量值，则可直接计算精确度。

^{公式4：计算精确度。}

例如，如果正在监测1 V的恒定电压，并且注意到测量值在两次测量之间变化了20 µV，则可按如下方式计算测量精确度： 

精确度通常以百分比表示。本例中精确度为99.998%。

精确度主要在需要进行设备校准等相对测量（相对于之前相同值的读数）时才有意义。

切勿将灵敏度与分辨率和代码宽度混淆。其中分辨率定义了代码宽度；这是仪器显示值的离散级别。而灵敏度则定义仪器记录值变化所需的电压变化。例如，测量范围为10 V的仪器也许能够以1 mV分辨率检测信号，但它可以测量的最小可检测电压可能为15 mV。这种情况下仪器的分辨率为1 mV，灵敏度为15 mV。

热噪声

理想电子电路本身不产生噪声，因此理想电路的输出信号仅包含原始信号中的噪声。但实际的电子电路和组件本身确实会产生一定程度的固有噪声。即使是简单的定值电阻也有噪声。 

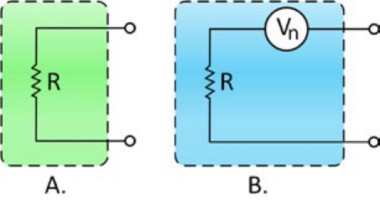
^{图4：图A所示为理想电阻，但实际上电阻具有内部热噪声，如B所示。}

图4A所示为理想无噪声电阻的等效电路。固有噪声在图4B中由噪声电压电源Vn与理想无噪声电阻Ri串联表示。在绝对零度（0°K或约-273 ℃）以上，任何材料中的电子都处于恒定的随机运动中。然而，由于该运动固有的随机性，在任何一个方向上都无法检测到电流。换句话说，电子在任何单一方向上的漂移在短时间内都会被相反方向的相等漂移抵消。因此，从统计学观点来说，电子运动是去相关的。然而，材料中会产生一系列连续的随机电流脉冲，这些脉冲被外界视为噪声信号。该信号有多种名称：约翰逊噪声、热激噪声或热噪声。该噪声随温度和电阻的增加而呈平方根函数增加。这意味着必须将电阻增加4倍才能使电阻的噪声增加1倍。

闪烁或¹/_F噪声 

半导体设备的噪声往往与频率不一致。它在频率较低时上升。这称为¹/_F噪声、粉红色噪声、过量噪声或闪烁噪声。此类噪声也存在于除电气系统之外的许多物理系统中。例如蛋白质、认知过程的反应时间，甚至地震活动。下图所示最可能的噪声源，具体取决于特定电压下噪声发生的频率；了解噪声产生的原因有助于降低噪声。

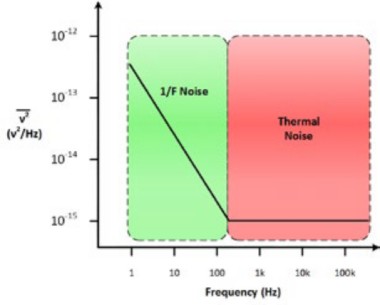
^{图4：图A所示为理想电阻，但实际上电阻具有内部热噪声，如B所示。}

尽管噪声对设计人员来说是一个严重的问题，尤其是在信号电平较低的情况下，但一些常识性方法可最大限度地减少噪声对系统的影响。以下是一些有助于降低噪声的策略：

• 保持电源电阻和放大器输入电阻尽可能低。使用高阻值电阻会成比例地增加热噪声。
• 总热噪声也是电路带宽的函数。因此，将电路带宽降至最低也能尽可能降低噪声。但须谨慎进行，因为必须保留信号的傅立叶频谱以便进行精确测量。该解决方案是将带宽与输入信号所需频率响应相匹配。
• 通过适当使用接地、屏蔽、布线、仔细放置电线以及滤波，防止外部噪声影响系统性能。
• 在系统的输入阶段使用低噪声放大器。
• 对于某些半导体电路，使用适用的最低直流电源电压。

• 灵敏度是输入信号可引起测量设备响应的最小变化。
• 精度是一个度量项，反映了仪器如实指示测量信号值的能力。
• 产品规范文档中会描述精度和灵敏度；由于不同公司和同一公司的不同产品可能对这些术语有不同的理解，请务必查看文档，并在需要时联系公司以获取说明。
• 精确度定义为测量仪器的稳定性及其对同一输入信号反复进行相同测量的能力。
• 噪声是干扰有用信号的所有无用信号。
• 有不同类型的噪声和多种降噪策略。

• 了解降低噪声的接地技术
• 了解抗混叠滤波器的工作原理
• 了解适用于自动特性分析、验证和生产测试的NI PXI DMM、示波器和DAQ设备
• 下载所有仪器基础知识内容
• 精度、代码宽度和分辨率位数之间的差异