QZ Decomposition VI

Owning Palette: Linear Algebra VIs

Requires: Multicore Analysis and Sparse Matrix Toolkit

Computes the QZ decomposition of a pair of matrices A and B.

Wire data to the A and B inputs to determine the polymorphic instance to use or manually select the instance.

Details  

QZ Decomposition (DBL)

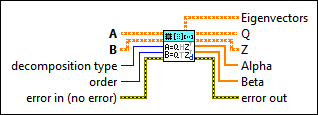
	A specifies the first square matrix. A and B must be the same size.
	B specifies the second square matrix. A and B must be the same size.
	decomposition type specifies the type of decomposition. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta, and the corresponding Eigenvectors, Q, and Z. order is valid only when decomposition type is Generalized Schur. 0 No Reorder (default)—Specifies that this VI does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to their real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to their real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to their magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to their magnitudes.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q returns an orthogonal matrix. Let trans(Q) represent the transpose matrix of Q, then Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z returns an orthogonal matrix. Let trans(Q) represent the transpose matrix of Q, then Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	error out contains error information. This output provides standard error out functionality.

QZ Decomposition (SGL)

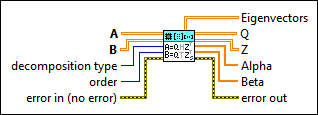
	A specifies the first square matrix. A and B must be the same size.
	B specifies the second square matrix. A and B must be the same size.
	decomposition type specifies the type of decomposition. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta, and the corresponding Eigenvectors, Q, and Z. order is valid only when decomposition type is Generalized Schur. 0 No Reorder (default)—Specifies that this VI does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to their real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to their real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to their magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to their magnitudes.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q returns an orthogonal matrix. Let trans(Q) represent the transpose matrix of Q, then Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z returns an orthogonal matrix. Let trans(Q) represent the transpose matrix of Q, then Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or a quasi-triangular matrix with 1-by-1 and 2-by-2 diagonal blocks if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	error out contains error information. This output provides standard error out functionality.

QZ Decomposition (CDB)

	A specifies the first square matrix. A and B must be the same size.
	B specifies the second square matrix. A and B must be the same size.
	decomposition type specifies the type of decomposition. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta, and the corresponding Eigenvectors, Q, and Z. order is valid only when decomposition type is Generalized Schur. 0 No Reorder (default)—Specifies that this VI does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to their real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to their real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to their magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to their magnitudes.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q returns a unitary matrix. Let trans(Q) represent the conjugate transpose matrix of Q, then Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z returns a unitary matrix. Let trans(Q) represent the conjugate transpose matrix of Q, then Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	error out contains error information. This output provides standard error out functionality.

QZ Decomposition (CSG)

	A specifies the first square matrix. A and B must be the same size.
	B specifies the second square matrix. A and B must be the same size.
	decomposition type specifies the type of decomposition. 0 Generalized Hessenberg (default) 1 Generalized Schur
	order specifies how to order the generalized eigenvalues, Alpha and Beta, and the corresponding Eigenvectors, Q, and Z. order is valid only when decomposition type is Generalized Schur. 0 No Reorder (default)—Specifies that this VI does not change the order of the generalized eigenvalues. 1 Real Ascending—Lists the generalized eigenvalues in ascending order according to their real parts. 2 Real Descending—Lists the generalized eigenvalues in descending order according to their real parts. 3 Magnitude Ascending—Lists the generalized eigenvalues in ascending order according to their magnitudes. 4 Magnitude Descending—Lists the generalized eigenvalues in descending order according to their magnitudes.
	error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
	Eigenvectors returns a complex matrix that contains the generalized eigenvectors in its columns.
	Q returns a unitary matrix. Let trans(Q) represent the conjugate transpose matrix of Q, then Q satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Z returns a unitary matrix. Let trans(Q) represent the conjugate transpose matrix of Q, then Z satisfies the following conditions: trans(Q)AZ is an upper Hessenberg matrix if the decomposition type is Generalized Hessenberg; or an upper triangular matrix if the decomposition type is Generalized Schur. trans(Q)BZ is an upper triangular matrix.
	Alpha returns the numerators of the generalized eigenvalues of matrix pair (A, B). If Beta is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	Beta returns the denominators of the generalized eigenvalues of matrix pair (A, B). If Betai is nonzero, Alphai/Betai is a generalized eigenvalue of (A, B).
	error out contains error information. This output provides standard error out functionality.

QZ Decomposition Details

The following table lists the support characteristics of this VI.

Supported on RT targets	Yes
Suitable for bounded execution times on RT	Yes

Refer to the Details section in the QZ Decomposition VI for more details about this VI.