PID 控制器與理論說明
綜覽
如同該名稱所表示,PID演算法包含 3 個筆基本係數:比例 (proportional)、積分 (integral)與微分 (derivative),可將之調整以獲得最佳響應。本文將探討閉迴路系統、傳統 PID 的理論以及調整閉迴路控制系統的效果。LabVIEW 中的 PID 工具組以及這些 VI 的易用性也會被討論。
內容
PID 控制系統
PID 控制器是一種儀器,能接收感測器輸入資料、計算實際值與理想設定值之間的差,再以調整輸出的方式控制溫度、流速、速度、壓力和電壓之類的變數。其運作原理是透過三種機制:對目前誤差產生反應的比例控制;消除過去累積之誤差的積分控制:以及預測未來誤差的微分控制。PID 控制器會加總這三項,據以計算輸出。這樣的架構讓 PID 控制器能夠有效率地維持流程控制與系統穩定性。 開始定義 PID 控制器的參數之前,先來了解閉迴路系統的概念與相關術語。
閉迴路系統
在標準控制系統中,流程變數是需要控制的系統參數,例如溫度 (ºC)、壓力 (psi) 或流量 (liters/min)。感測器可用來量測流程變數,並向控制系統提供反饋。設定點是流程變數的所需或指令值,例如溫度控制系統中為 100 歐氏度。任何時候,控制系統演算法 (補償器) 都會使用流程變量與設定點之間的差異,以決定所需的執行器輸出,並驅動系統 (機器)。例如,如果量測的溫度流程變量為 100 ºC,而所需的溫度設定點為 120 ºC,則由控制演算法指定的致動器輸出可能是驅動加熱器。驅動致動器以啟動加熱器時,系統溫度會升高,因而會增加溫度流程變量。這種方式稱為閉迴路控制系統,因為讀取傳感器提供恆定反饋和計算所需致動器輸出的過程被連續重複並以固定的迴路速率進行,如圖 1 所示。
在許多情況下,致動器輸出不是對系統產生影響的唯一信號。例如,溫度室中可能存在一個冷空氣來源,有時會吹入溫度室並干擾溫度。這種用語也稱為干擾。我們通常嘗試設計控制系統,以盡量減少干擾對製程變數的影響。
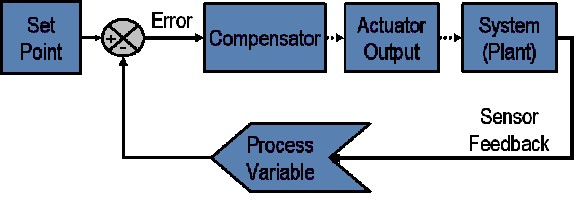
圖 1:典型閉迴路系統的程式方塊圖。
術語定義
控制設計流程從定義效能需求開始。控制系統效能通常會透過將步驟函式應用為設定點指令變數,然後量測流程變數的響應來量測。通常情況下,通過測量定義的波形特性來量化響應。上升時間是系統從穩定狀態或最終值的 10% 升至 90% 所用的時間。百分比過衝是處理變數過衝最終值的量,以最終值的百分比表示。靜態時間是流程變量在最終值的特定百分比 (通常是 5%) 內結算所需的時間。穩定狀態誤差是流程變數與設定點之間的最終差異。請注意,這些數量的確切定義將因業界和學術界而異。
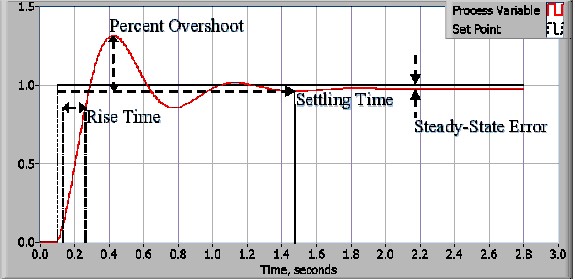
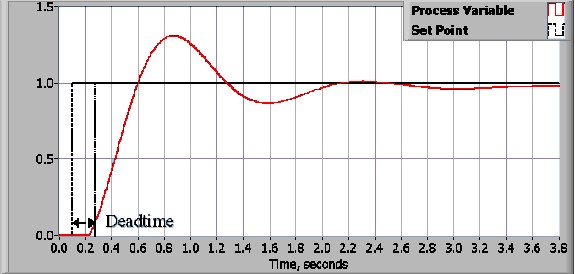
一旦指定了效能需求,即可檢查系統,並可選擇合適的控制方式。在大多數應用中,PID 控制將提供所需的結果
PID 理論
比例響應
比例分量僅取決於設定點和流程變數之間的差異。此差異可稱為「錯誤」項目。比例增益 (Kc) 決定輸出響應與誤差信號的比率。例如,如果錯誤項的幅度為 10,則比例增益為 5 會產生 50 的比例回應.一般而言,增加比例增益會提高控制系統的響應速度。但是,如果比例增益太大,則流程變量會開始發振。若將 Kc 進一步增加,振動會越來越大,並且系統會變得不穩定,甚至可能會發生無法控制的振動。

積分響應
積分成分會隨著時間的推移加上錯誤項。結果是,即使是一個很小的錯誤術語,也會導致積分成分緩慢增加。除非誤差為零,否則積分響應會隨著時間的遷移不斷增加,因此效果是將穩態誤差驅動至零。穩定狀態誤差是流程變數與設定點之間的最終差異。當整合動作使控制器飽和,而控制器無法將錯誤訊號推向零時,就會發生一個稱為整合 windup 的現象。
微分響應
若流程變量快速增加,微分元件會導致輸出量降低。微分響應與流程變量的變化速率成比例。增加微分時間 (Td),參數可讓控制系統對錯誤項的變化進行更強烈的反應,並提升整體控制系統的響應速度。大多數實用的控制系統使用極小的微分時間 (Td),因為微分響應對流程變量訊號中的噪聲非常敏感。如果傳感器反饋信號嘈雜或控制迴路速率太慢,微分響應可能會使控制系統變得不穩定
調整
為 P、I 與 D 設定最佳增益,以便取得控制系統的理想響應,這個流程被稱為調整。 PID 調整方法不只一種,本文探討的會是其中的「猜測與檢驗」(guess and check)方法和「齊格勒尼科爾斯」(Ziegler Nichols) 方法。
PID 控制器的增益可以通過試錯法獲得。一旦工程師了解每個增益參數的重要性,這種方法就變得相對容易了。在此方法中,先將 I 與 D 項設為零,並增加比例增益直到迴路的輸出振盪。隨著比例增益的增加,系統也會更快速作業,但必須注意,不要使系統變得不穩定。一旦 P 被設置為獲得所需的快速響應,積分項就會增加以停止振盪。積分術語減少了穩態誤差,但增加了過衝。快速系統總需要一定量的過衝,以便它可以立即響應更改。調整積分項以實現最小的穩態誤差。一旦 P 和 I 被設置為以最小的穩態誤差獲得所需的快速控制系統,微分項就會加大,直到迴路能夠快速達到設定點。增加微分項會降低過衝並產生更高的增益和穩定性,但會使系統對雜訊高度敏感。通常,工程師需要權衡控制系統的一個特性,以便更好地滿足他們的要求。
Ziegler-Nichols 方法是 PID 控制器調整的另一種常見方法。這種方法與試錯法非常相似,其中 I 和 D 被設置為零,而 P 會增加,直到迴路開始振動。振動開始後,注意臨界增益 Kc 和振盪 Pc 的週期。接著,P、I 與 D 會按照下表列調整。
控制
| P
| Ti
| Td
|
P
| 0.5Kc
| -
| -
|
PI
| 0.45Kc
| Pc/1.2
| -
|
PID
| 0.60Kc
| 0.5Pc
| Pc/8
|
NI LabVIEW 與 PID
LabVIEW PID 工具組包含多種 VI,對於基於 PID 的控制系統的設計非常有幫助。控制輸出範圍限制,用於 PID 增益變化的集成器防發條和無罩式控制器輸出是 PID VI 的一些顯著特色。PID 進階 VI 包含 PID VI 的所有功能,以及非線性積分動作、雙自由度控制與誤差平方控制。

圖 5:源於 LabVIEW PID 控制面板的 VI
PID 面板也包含一些進階 VI,例如 PID Autotuning VI 與 PID Gain Schedule VI。PID Autotuning VI 可協助精確控制系統的 PID 參數。一旦對 P、I 與 D 的值進行熟悉的推測,「PID 自動調整」VI 有助於完善 PID 參數以從控制系統獲得更好的響應。

使用在即時目標上執行的 LabVIEW Real Time 模組,可大幅提升控制系統的可靠性。NI 提供資料擷取裝置,相比平均控制系統可提供更高準確度與更高效能
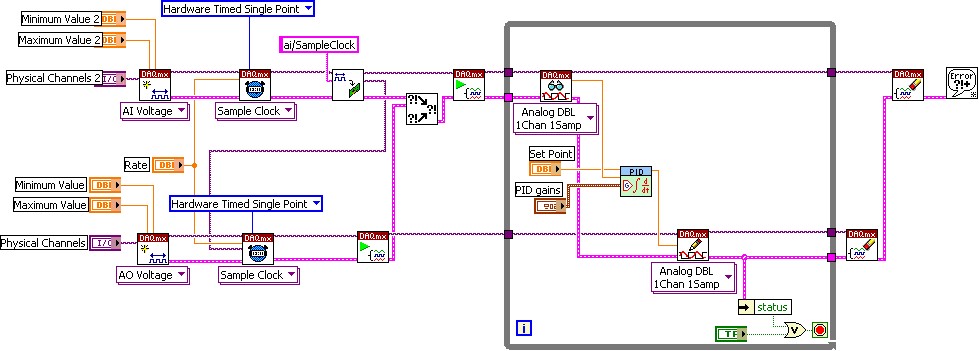
圖 7:顯示著含 NI 資料擷取裝置外掛的 PID 控制的典型 LabVIEW VI
這些資料擷取裝置與 LabVIEW 緊密整合,可最小化所需的開發時間,並大幅提升任意一位工程師的生產力。[圖 7] 顯示 LabVIEW 中的典型 VI,顯示使用 NI-DAQmx 驅動程式 API 的 PID 控制,該應用程式包含在 NI 資料擷取硬體中。
摘要
PID 控制演算法是一種強大而簡單的算法,在行業中廣泛使用。此演算法具有足夠的靈活性,可在多種應用中取得出色的結果,而且一直是多年來持續使用的主要原因之一。NI LabVIEW 與 NI 插件資料擷取裝置具有更高的準確度與效能,可用作出色的 PID 控制系統。
參考資料
1.傳統 PID 控制
by Graham C. Goodwin、Stefan F. Graebe、Mario E. Salgado
控制系統設計、Prentice Hall PTR
2.連續流程的 PID 控制
by John W. Webb Ronald A. Reis
可程式化邏輯控制器、第四版、Prentice Hall PTR