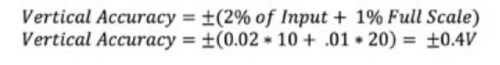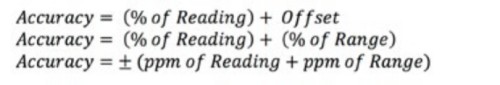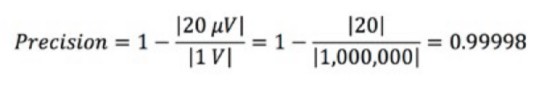類比樣本品質:準確度、靈敏度、精確度與雜訊
綜覽
學習靈敏度、準確度、精確度與雜訊相關知識,從而了解並改善量測樣本品質。
內容
量測靈敏度
要講求樣品品質,就要評估量測準確度與精確度。不過,重點在於要先了解示波器的靈敏度。靈敏度是輸入訊號中會讓量測裝置出現反應的最小變化。換句話說,如果輸入訊號變化達到定量 (達到特定靈敏度),數位資料就會呈現出變化。
請勿將靈敏度、解析度與程式碼寬度混淆。解析度定義的是程式碼寬度;這是儀器顯示數值的離散程度。而靈敏度定義的則是要讓儀器記錄數值變化所需達到的電壓變化。例如,量測範圍是 10 V 的儀器,或許能夠偵測到解析度是 1 mV 的訊號,但這台儀器所能量測到的最小電壓可能會是 15 mV。在這個情況下,這台儀器的解析度是 1 mV,而靈敏度卻是 15 mV。
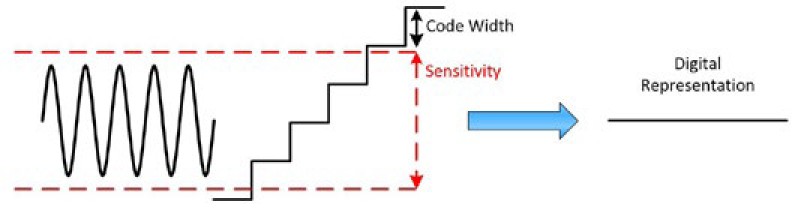
在某些情況下,靈敏度會大於碼寬。起初看似不合理,這難道不是代表電壓變化達到可以顯示但不能記錄的量嗎?是!想想 DC 恆壓就能了解其優點。電壓若能保持絕對穩定且不發生任何偏差,自然再好不過,但訊號必定會出現微小的變化,就如圖 1 所示。紅色實線表示靈敏度,圖中另也顯示出碼寬。在此範例中,由於電壓絕對不會高於靈敏度,因此,即便電壓大於碼寬,仍會以同一個數值表示。這樣的優點在於不會擷取到雜訊,且能更準確地以恆壓呈現訊號。
圖 1:靈敏度大於碼寬有助於消除雜訊。
一旦訊號確實開始上升,則會高於靈敏度,之後就以另一個數值表示。請見圖 2。請注意,量測值絕對不會比靈敏度更準確。
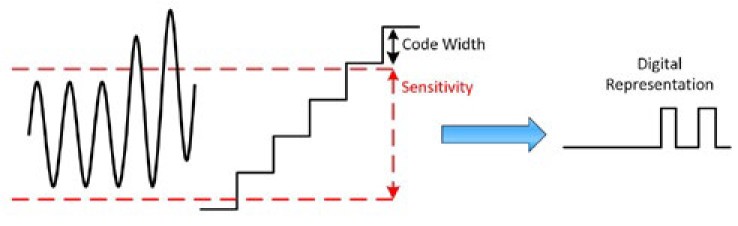
圖 2:一旦訊號高於靈敏度,就會以另一個數值表示。
儀器靈敏度的定義方式也並非十分明確。有時可以如上方範例所示,將靈敏度定義為固定量。在此情況下,一旦輸入訊號高於靈敏度,就會以另一個數值表示訊號。不過,有時候也可以將靈敏度定義為訊號的變化。當訊號變化量達到一定的靈敏度之後,就會以另一個訊號表示。在此情況下,重要的並不是絕對電壓,而是電壓的變化。此外,有些儀器的靈敏度定義在 0 左右。
不同公司對於靈敏度一詞的確切定義不盡相同,即便是同公司生產的不同產品,對於靈敏度一詞的使用方式也略有不同。請務必參閱儀器規格,確實了解靈敏度的定義方式;倘若沒有具體說明,請向生產儀器的公司洽詢。
準確度
準確度的定義是儀器準確指示受測訊號值的功能指標。準確度與解析度無關;不過,準確度絕對不會優於儀器的解析度。
依據儀器或示波器的不同,準確度期望值也會不一樣。舉例來說,數位電錶 (DMM) 的準確度通常應要高於示波器的準確度。準確度的計算方式也因裝置而異,但請務必確認儀器的規格,實際了解儀器計算準確度的方式。
示波器的準確度
示波器會分別定義水平和垂直系統的準確度。水平系統是指時間刻度或 X 軸;水平系統準確度就是時基準確度。垂直系統是測得的電壓或 Y 軸;垂直系統準確度則是增益與偏移準確度。垂直系統準確度的重要性通常高於水平系統準確度。
垂直準確度通常以輸入訊號的百分比與最大量測範圍的百分比表示。某些規格會將輸入訊號細分為垂直增益和偏移準確度。方程式 1 顯示兩種不同的準確度定義方式。
方程式 1:計算示波器的垂直準確度。
比方說,示波器的垂直準確度定義方式可能分為以下幾種:
在輸入訊號為 10 V 且使用範圍是 20 V 的情況下,即可計算準確度:
DMM 與電源供應器的準確度
DMM 與電源供應器通常是按讀數百分比指定準確度。方程式 2 顯示 DMM 或電源供應器準確度的三種不同表示方式。
方程式 2:計算 DMM 或電源供應器的垂直準確度。
ppm 是指百萬分比。多數規格會附多份用於判斷準確度的表格。準確度取決於量測類型、範圍,以及上次校準至今經過的時間。請參閱您所用的規格,實際了解準確度計算方式。
舉例來說,將 DMM 的範圍設為 10 V,校準後在 23 °C ±5 °C 的溫度條件下運作 90 天,預期訊號會是 7 V。這些條件的準確度規格註明是 ±(讀數 20 ppm + 範圍 6 ppm)。於是可以計算準確度:
此時,讀數應介於實際輸入電壓的 200 μV 以內
DAQ 裝置的準確度
DAQ 介面卡的準確度定義通常是相較於理想傳輸功能的偏差值。方程式 3 舉例說明 DAQ 介面卡指定準確度的方式。
方程式 3:計算 DAQ 裝置的準確度。
接著分別定義各個術語:
這類術語的定義大多列於表格中,並以標稱範圍為準據。其規格也定義雜訊不確定性的計算方式。雜訊不確定性是指量測中由於雜訊影響而造成的量測不確定性,也是決定準確度時要考慮的因素。
此外,裝置可能適用多個準確度表,端視您所要求的是類比輸入準確度或類比輸出準確度,也取決於是否啟用或停用了某個濾波器。
精確度
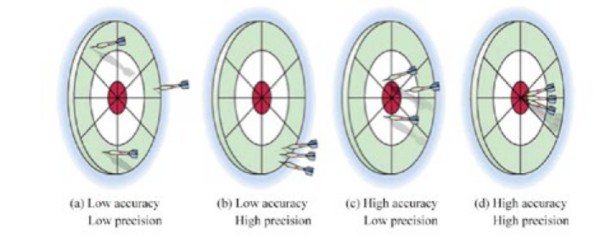
準確度和精確度通常可以互換通用,但仍有細微差別。精確度的定義是儀器的量測穩定性,以及重複輸入相同訊號時能否讓量測結果保持一致。準確度是指量測值與實際值之間的相近程度,而精確度則是指每一次重複量測彼此之間的相近程度。
圖 3:精確度與準確度相關但不相同。
精確度主要受儀器的雜訊和短期漂移影響。通常我們無法直接得知儀器的精確度,必須根據傳輸比規格、雜訊以及溫度漂移等其他規格進行推算。不過,只要能掌握一系列的量測結果,就能計算精確度。
方程式 4:計算精確度。
舉例來說,若在監控 1 V 的恆壓時留意到不同次量測的量測值出現了 20 µV 的變化,則可按照以下方式計算量測精確度:
精確度通常以百分比表示。這個範例的精確度是 99.998%。
需要進行如裝置校準之類的相對量測 (相對於同一個值之前的讀數) 時 ,精確度就特別重要。
雜訊與雜訊源
請勿將靈敏度、解析度與程式碼寬度混淆。解析度定義的是程式碼寬度;這是儀器顯示數值的離散程度。而靈敏度定義的則是要讓儀器記錄數值變化所需達到的電壓變化。例如,量測範圍是 10 V 的儀器,或許能夠偵測到解析度是 1 mV 的訊號,但這台儀器所能量測到的最小電壓可能會是 15 mV。在這個情況下,這台儀器的解析度是 1 mV,而靈敏度卻是 15 mV。
熱雜訊
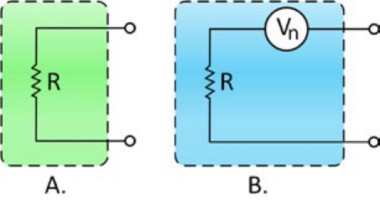
理想的電子電路並不會自行產生雜訊,因此,理想電路的輸出訊號只含原始雜訊中的訊號。不過,實際的電子電路與元件確實會自行產生一定程度的雜訊。即便是簡易的固定值電阻器也會產生雜訊。
圖 4:A 代表理想的電阻器,但實際上,電阻器是具有內部熱雜訊的,如 B 所示。
圖 4A 顯示理想無雜訊電阻器的等效電路。圖 4B 以雜訊電壓源 Vn 表示原有雜訊,另有理想的無雜訊電阻 Ri。只要溫度高於絕對零度 (0°K 或 -273°C),任何物質中的電子都會保持著永恆無規則運動。不過,由於這樣的運動具有無規則特性,因此在任何一個方向均無法測得電流。換句話說,單向電子漂移一律會被反向的等效漂移暫時抵銷。也因為如此,電子運動在統計方面的相關性並不存在。不過,物質仍會持續隨機產生電流脈衝,而外部所觀察到的這類脈衝即成為所謂的雜訊。這種訊號有幾個不同的名稱:強森雜訊 (Johnson Noise)、熱騷動雜訊 (Thermal Agitation Noise),或是熱雜訊 (Thermal Noise)。這種雜訊會隨著溫度和電阻而增加,但會是平方根函數。因此,您必須將電阻增為四倍,才能將電阻器的雜訊增為兩倍。
閃爍 (Flicker) 或 1/F 雜訊
半導體裝置通常會產生頻率不穩定的雜訊。這樣的雜訊會在低端升高。這就稱為 1/F 雜訊、粉紅雜訊、過量雜訊或閃爍雜訊。不只電機系統,許多物理系統也會發生這類雜訊。範例包括蛋白質、認知歷程的反應時間,甚至包括地震活動。下圖以特定電壓發生的雜訊頻率為據,顯示可能性最高的雜訊來源;知道雜訊的成因對降低雜訊十分有幫助。
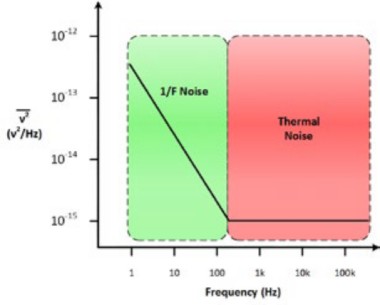
圖 4:A 代表理想的電阻器,但實際上,電阻器是具有內部熱雜訊的,如 B 所示。
降低雜訊的策略
雖然雜訊對設計師而言是嚴重的問題,出現低訊號位準時尤其如此,但已經有許多常見方式能夠降低雜訊對系統的影響。以下列舉一些有助於降低雜訊的策略:
- 電源電阻與放大器輸入電阻越低越好。電阻的值越高,熱雜訊就越高。
- 整體熱雜訊也是電路頻寬的其中一項功能。因此,盡可能降低電路頻寬也能盡量減少雜訊。但若要降低電路頻寬,必須審慎為之,因為必須保留訊號的傅立葉頻譜,才能進行準確量測。解決之道是讓頻寬符合輸入訊號所要求的頻率響應。
- 要避免外部雜訊影響系統效能,則可視情況使用接地、抗雜訊以及接線等方式,並且仔細佈線與濾波。
- 在系統的輸入階段使用低雜訊放大器。
- 使用某些半導體電路時,請使用符合作業需求範圍內的最低 DC 電源供應電位。
摘要
- 靈敏度是輸入訊號中會讓量測裝置出現反應的最小變化。
- 準確度的定義是儀器準確指示受測訊號值的功能指標。
- 準確度和靈敏度均記載於規格文件中;由於不同公司 (以及同公司的不同產品) 所用的術語未必相同,因此,請務必參閱說明,如有需要請向公司洽詢。
- 精確度的定義是儀器的量測穩定性,以及重複輸入相同訊號時能否讓量測結果保持一致。
- 雜訊是可能干擾所需訊號的無用訊號。
- 雜訊分為許多不同的類型,也有許多不同的策略有助於降低雜訊。
後續步驟
- 了解能降低雜訊的接地技術
- 了解抗混疊濾波器的運作原理
- 了解適用於自動化特性分析、驗證與生產測試的 NI PXI DMM、示波器以及 DAQ 裝置。
- 下載所有儀器基本原理內容
- 準確度、程式碼寬度與解析度位元之間的差異