NI SourceAdapt技术:新一代SMU技术
概览
源测量单元(SMU)是用于测试各种设备的电流电压(I-V)特性的重要仪器。设备范围涵盖了从晶体管等电子元器件到随身听等集成电子产品,乃至医疗器械。NI SourceAdapt技术源自NI,作为4通道NI PXIe-414x精密SMU系列产品的代表首次亮相。该技术是基于数字控制循环(而非传统模拟控制循环)的新一代技术。借助NI SourceAdapt技术,您可以针对任意负载自定义响应,从而实现最短上升时间内的理想响应,且无过冲或振荡。所有NI精密系统SMU、PXI电子负载模块和PXI可编程电源的特定选项均配有NI SourceAdapt。 让我们来了解一些SourceAdapt技术的幕后故事。本文将主要讨论与SMU相关的SourceAdapt操作,其工作方式与PXI电子负载模块或PXI可编程电源相同。
内容
概述
SMU采用闭环反馈控制,以确保编程的源值(设定值)正确地应用于待测负载。传统的SMU使用模拟硬件来实现控制循环,但是这种方式有利有弊。例如,针对高速测试的高带宽SMU通常不适合用于测试需要高稳定性的高电容负载。另一方面,针对高电容负载测试的SMU可能也不是高速测试的最佳选择。事实上,大多数传统的SMU通常已经针对高速测试或高稳定性测试进行了优化设计。即使如此,获得最佳响应仍然难以实现,因为设计刚好能为不同负载提供正确响应的电路本就困难重重。
NI SourceAdapt技术可帮助您自定义调整针对给定负载的SMU响应,从根本上解决了这个问题。这实现了最佳SMU响应与最短稳定时间,从而缩短了等待时间和测试时间。此外,该技术不仅消除了过冲进而保护待测设备(DUT),而且也消除了振荡,得以保证系统的稳定性。
由于SMU响应的调整是通过编程完成的,您可以轻松地将针对高速测试的SMU重新配置为针对高稳定性测试的单元-从而最大化您的测试设备投资回报,并获得更好的测试结果。
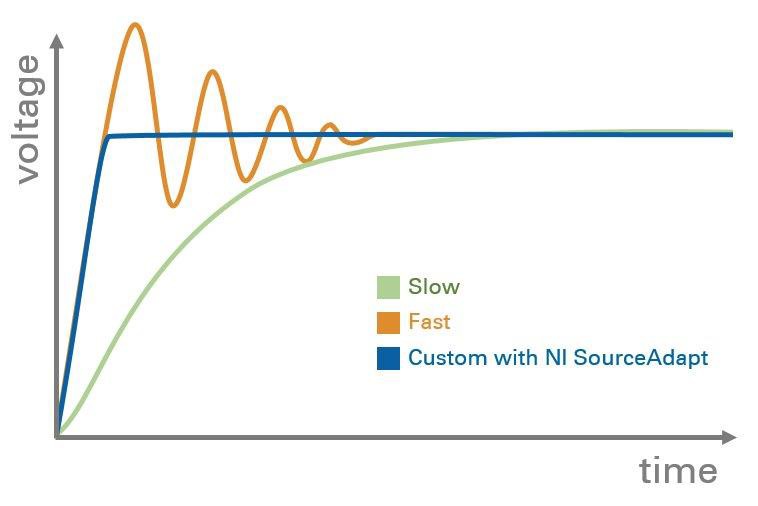
图1.SMU的电容负载响应。借助于NI SourceAdapt技术,您可以自定义响应(红线所示),以实现最大稳定性和最短瞬态响应时间。
传统模拟控制循环的局限性
过去,测试仪器供应商采取了不同的方法来实现可配置的传递函数。在传统的方式中,供应商在控制循环的反馈路径内外引入了切换电抗元件。该方法受限于其效果、可配置性以及可扩展性。在SourceAdapt技术可实现的范围内,真正的自定义补偿需要我们彻底重新思考如何构建SMU控制循环。
SMU的控制循环是两个闭合控制循环的叠加:一个电流闭环和一个电压闭环。图2a展示了传统SMU的架构理念。
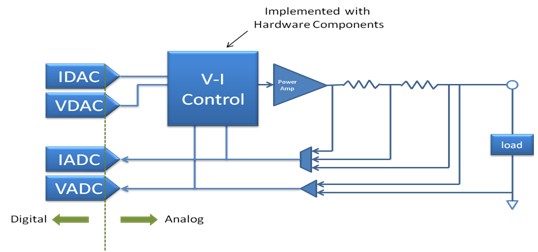
图2a.传统SMU的架构简图。注意:控制循环(V-I Control)是采用模拟硬件组件实现的,因此可配置性非常有限。
V-I Control为电流和电压赋予了设定值,其闭环反馈机制可以精确地控制输出电压和电流,使其符合设定值。整个控制循环是借助于放大器和其他一些有源模拟硬件来实现的。反馈信号由模数转换器(ADC)读取,以提供高精度测量。如要改变这种架构的补偿模式,则需要添加分立的电抗组件。从某种程度上说,您可以通过开关以编程方式进行此类调整,但这种方法具有局限性和缺陷。最多只能让您从几个可能实现的配置方案中选择一个来实施。这并不能满足针对给定负载优化SMU响应的要求。那么,如何才能随心所欲地配置控制循环呢?答案就是:采用全新的架构(如图2b所示)。
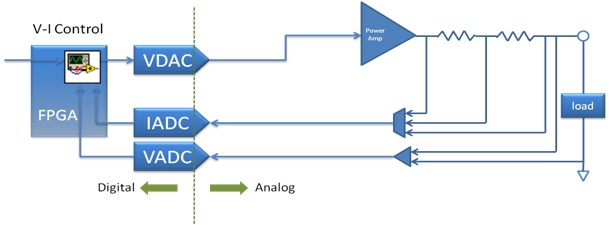
图2b.全新的NI SMU架构。注意:控制循环(V-I Control)已移至数字控制部分,且位于现场可编程门阵列(FPGA)内。
在这个新架构中,V-I Control移至数字控制部分,且位于FPGA内。不同于模拟控制循环,数字控制循环可完全通过软件进行配置,因而我们可以通过优化控制循环来实现针对现有负载的理想响应。控制循环的多样化实现方式使得SourceAdapt技术成为可能-提供针对任意负载的自定义SMU响应。
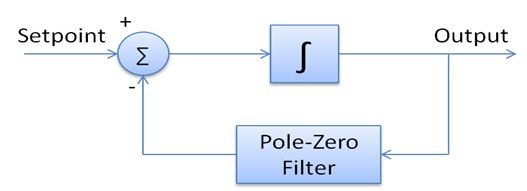
图3.全新的数字V-I Control实现模式
V-I Control包含一个积分器(用于为回路提供DC精确度和一般调节功能),以及一个用于实现自定义补偿的零极点滤波器。这两个模块都是用户可配置的,所具有的可配置性是模拟控制循环难以企及的。同时,借助于快速ADC和DAC,以及FPGA的处理能力,整个回路可完全满足精确源测量应用的需求。最终,我们实现了一个具备极强可配置性的架构,且无需牺牲性能。
了解SourceAdapt技术背后的架构
基于SourceAdapt技术,新架构通过两种方式实现了对传递函数的调节。第一,调节积分器的增益-带宽积(GBW);第二,将反馈补偿器作为超前或者滞后补偿器使用,这样您就可以在任意频率为传递函数添加零极点对。
增益-带宽调节
输出路径上的积分器提供了一个开环传递函数,外观类似于波特量(增益裕度[1])和相位裕度[2] 图上运算放大器的开环传递函数。
图4a.积分器开环传递函数(左:增益裕度;右:相位裕度)
图4b.空载输出时对应的1 V阶跃响应(对应图4a的传递函数)
通过调节积分器的增益或回路的GBW,您就可以调整回路的总体响应,使响应行为变得:
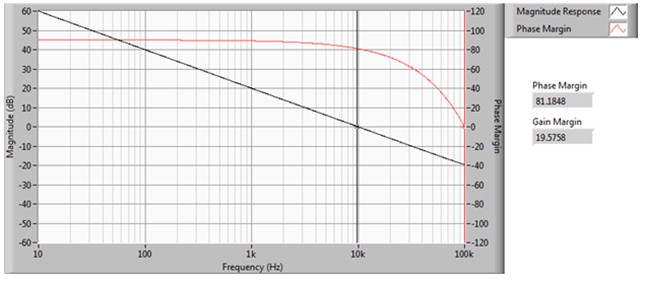
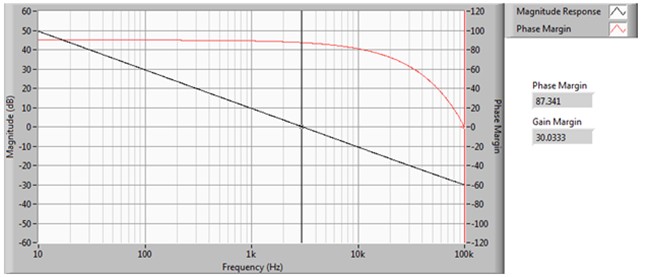
- 更慢但更稳定,例如,采用3 kHz的GBW和87.34的相位裕度(参见图5a和5b)
- 更快速,例如采用20 kHz的GBW(参见图6a和6b)
图5a.3 kHz GBW和87.34相位裕度时的响应较为缓慢,但更稳定
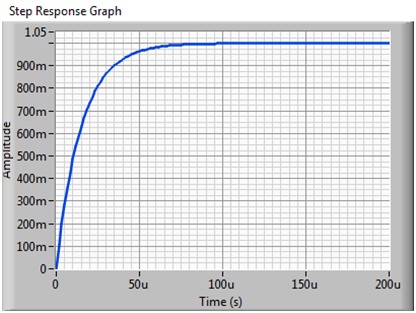
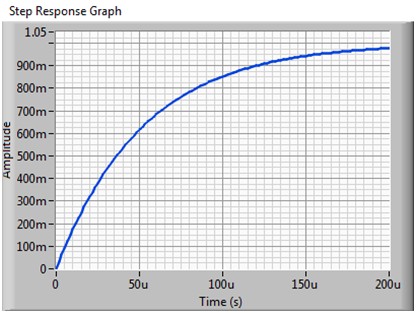
图5b.空载输出时对应的1 V阶跃响应(对应图5a的传递函数)
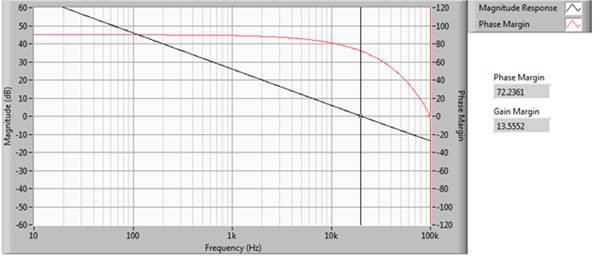
图6a.20 kHz GBW和72.23相位裕度时的响应较快速
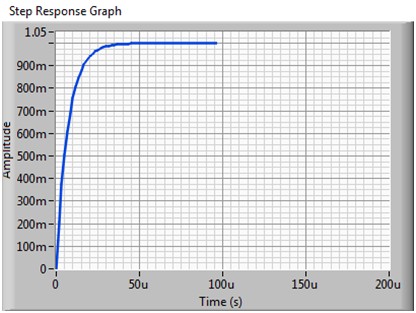
图6b.空载输出时对应的1 V阶跃响应(对应图6a的传递函数)
无功负载条件下
不稳定的无功负载更具挑战性,如果要使较不稳定的无功负载变得较为稳定,只需减慢回路的运行速度即可实现。图7a和7b显示了使用电容作为负载的控制循环的行为。电容器产生极性时的频率与电容和输出阶段分流电阻成反比,此时增益和相位也会受到影响。图7a展示了负载为0.1 µF电容时开环频率响应。图7b显示了相应的阶跃响应。
图7a.负载为0.1 µF电容时,开环传递函数临界稳定。
图7b.负载为0.1 µF电容时,对应的1 V阶跃响应
图7b所示的响应是欠阻尼响应,产生了过冲,且需要较长时间才能达到稳定状态。调节GBW可使系统的表现更佳。如果您最希望完全消除过冲,则可以将回路的运行速度减慢到足以获得响应而不产生任何过冲的程度。图8a和8b显示了在500 Hz GBW缓慢响应的情况下,可完全消除过冲。
图8a.500Hz GBW的开环传递函数(负载:0.1 µF电容)
图8b.500Hz GBW时对应的1 V阶跃响应(上升时间约为1 ms)
尽管已消除过冲,但系统响应变得很慢。为了获得最优响应,可采用第二种方法来调节传递函数:使用反馈补偿器(作为超前或者滞后补偿器)。
使用反馈补偿器
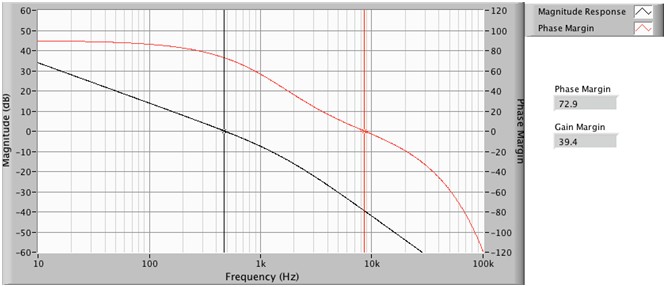
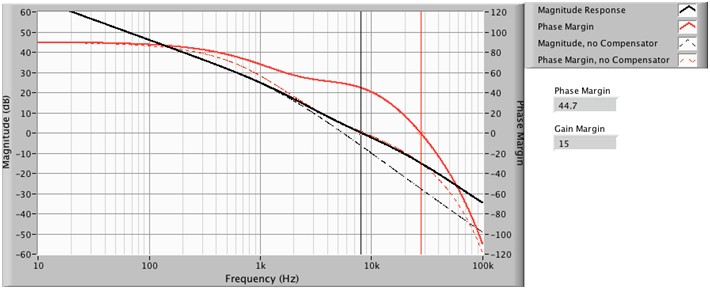
SourceAdapt技术提供了另一种优化响应的工具:反馈补偿器。我们继续沿用前面的例子,我们的目标是实现较短的上升时间的同时避免过冲和振荡。这个可以通过使用补偿器来抵消由电容器产生的极效应来实现。通过这种控制,我们可以进一步增大GBW,在保持稳定的同时亦可获得更短的上升时间。图9a显示当GBW增加到20 kHz时,使用补偿器与不使用补偿器两种情况下的增益裕度和相位裕度响应的对比。
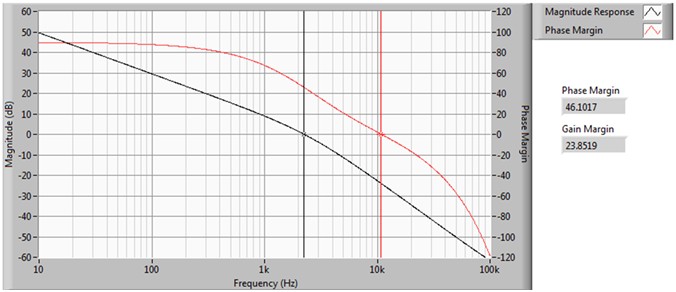
图9a.有无补偿器时的开环传递函数对比(GBW:20 kHz;负载:0.1 µF电容)
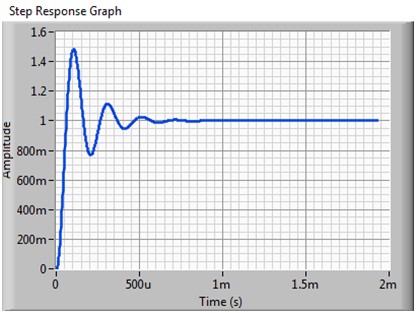
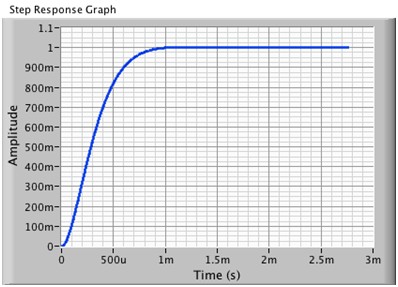
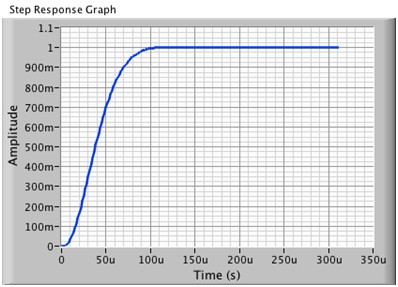
图9b.GBW为20 kHz且使用补偿器时对应的1 V阶跃响应(上升时间:~100 µs)
如图9b所示,此响应非常理想:上升时间减少了10倍且无过冲;相位裕度约为45度,稳定性极佳。
借助SMU来实现理想响应
由于负载可直接影响源测量单元(SMU)控制循环的传递函数,因此,由此可见,要获得理想的响应,给定负载需具备可配置性。借助于NI SourceAdapt技术,您可以针对任意负载自定义SMU响应,从而实现最短上升时间内的理想响应,且无过冲或振荡。这意味着您可以更快地进行测试,而不会出现可能的待测设备损坏或破坏系统稳定性的风险。