Particle Measurements
- Updated2023-05-01
- 13 minute(s) read
This section contains tables that list and describe the NI Vision particle measurements. The tables include definitions, symbols, and equations for particle measurements.
 |
Note Some equation symbols may be defined inside tables later in the section. |
Particle Concepts
The following table contains concepts relating to particle measurements.
| Concept | Definition | ||
|---|---|---|---|
| Bounding Rect | Smallest rectangle with sides parallel to the x-axis and y-axis that completely encloses the particle.
|
||
|
Perimeter |
Length of a boundary of a region. Because the boundary of a binary image is comprised of discrete pixels, NI Vision subsamples the boundary points to approximate a smoother, more accurate perimeter. Boundary points are the pixel corners that form the boundary of the particle. Refer to the introduction for an illustration of pixel corners. | ||
| Particle hole | Contiguous region of zero-valued pixels completely surrounded by pixels with nonzero values. Refer to the particle holes section for more information. | ||
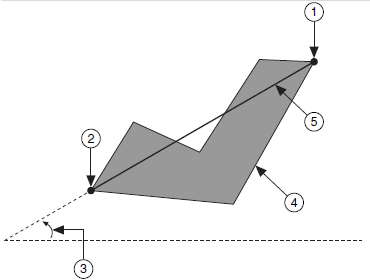
| Angle | Degrees of rotation measured counter-clockwise from the x-axis, such that 0 ≤ θ < 180. | ||
| Equivalent Rect | Rectangle with the same perimeter and area as the particle. | ||
| Equivalent Ellipse | Ellipse with the same perimeter and area as the particle. | ||
| Max Feret Diameter | Line segment connecting the two perimeter points that are the furthest apart.
|
||
|
Convex Hull |
Smallest convex polygon containing all points in the particle. The following figure illustrates two particles, shown in gray, and their respective convex hulls, the areas enclosed by black lines.
|
||
|
Max Horiz. Segment Length |
Longest row of contiguous pixels in the particle. This measurement is always given as a pixel measurement. | ||
| Sum | Moments of various orders relative to the x-axis and y-axis. | ||
| Moment of Inertia | Moments about the particle center of mass. Provides a representation of the pixel distribution in a particle with respect to the particle center of mass. Moments of inertia are shift invariant. | ||
| Norm. Moment of Inertia | Moment of Inertia normalized with regard to the particle area. Normalized moments of inertia are shift and scale invariant. | ||
| Hu Moment | Moments derived from the Norm. Moment of Inertia measurements. Hu Moments are shift, scale, and rotation invariant. |
Particle Holes
A particle hole is a contiguous region of zero-valued pixels completely surrounded by pixels with nonzero values. A particle located inside a hole of a bigger particle is identified as a separate particle. The area of a hole that contains a particle includes the area covered by that particle.
 |
|||
| Particle # | Area | Area of Hole | Area of Particle & Holes |
| 1 | A | B + C | A + B + C |
| 2 | D | 0 | D |
| 3 | E | F + G | E + F + G |
| 4 | G | 0 | G |
Hole measurements are valuable when analyzing particles similar to the one in figure A. For example, if you threshold a cell with a dark nucleus (figure A) so that the nucleus appears as a hole in the cell (figure B), you can make the following cell measurements:
- Area of Hole—Returns the size of the nucleus.
- Area of Particle and Hole—Returns the size of the entire cell.
- Area of Hole/Area of Particle and Hole—Returns the percentage of the cell that the nucleus occupies.

Coordinates
The following table lists the NI Vision particle measurements relating to coordinates.
| Measurement | Definition | Symbol | Equation |
|---|---|---|---|
| Center of Mass | Point representing the average position of the total particle mass, assuming every point in the particle has a constant density. The center of mass can be located outside the particle if the particle is not convex. | — | — |
| First Pixel | Highest, leftmost particle pixel. The first pixel is always given as a pixel measurement. The black squares in the following figure represent the first pixel of each particle. |
— | — |
| Center of Mass x | X-coordinate of the particle Center of Mass. | x | 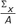 |
| Center of Mass y | Y-coordinate of the particle Center of Mass. | y |  |
| First Pixel x | X-coordinate of the first particle pixel. | — | — |
| First Pixel y | Y-coordinate of the first particle pixel. | — | — |
| Bounding Rect Left | X-coordinate of the leftmost particle point. | BL | — |
| Bounding Rect Top | Y-coordinate of highest particle point. | BT | — |
| Bounding Rect Right | X-coordinate of the rightmost particle point. | BR | — |
| Bounding Rect Bottom | Y-coordinate of the lowest particle point. | BB | — |
| Max Feret Diameter Start x | X-coordinate of the Max Feret Diameter Start. | Fx1 | — |
| Max Feret Diameter Start y | Y-coordinate of the Max Feret Diameter Start. | Fy1 | — |
| Max Feret Diameter End x | X-coordinate of the Max Feret Diameter End. | Fx2 | — |
| Max Feret Diameter End y | Y-coordinate of the Max Feret Diameter End. | Fy2 | — |
| Max Horiz. Segment Length Left | X-coordinate of the leftmost pixel in the Max Horiz. Segment. Max Horiz. Segment Length Left is always given as a pixel measurement. | — | — |
| Max Horiz. Segment Length Right | X-coordinate of the rightmost pixel in the Max Horiz. Segment. Max Horiz. Segment Length Right is always given as a pixel measurement. | — | — |
| Max Horiz. Segment Length Row | Y-coordinate for all of the pixels in the Max Horiz. Segment. Max Horiz. Segment Length Row is always given as a pixel measurement. | — | — |
Lengths
the following table lists the NI Vision particle relating to length.
| Measurement | Definition | Symbol | Equation | |||
|---|---|---|---|---|---|---|
| Bounding Rect Width | Distance between Bounding Rect Left and Bounding Rect Right. | W | BR – BL | |||
| Bounding Rect Height | Distance between Bounding Rect Top and Bounding Rect Bottom. | H | BB – BT | |||
| Bounding Rect Diagonal | Distance between opposite corners of the Bounding Rect. | — |

|
|||
| Perimeter | Length of the outer boundary of the particle. Because the boundary is comprised of discrete pixels, NI Vision subsamples the boundary points to approximate a smoother, more accurate perimeter. | P | — | |||
| Convex Hull Perimeter | Perimeter of the Convex Hull. | PCH | — | |||
| Hole Perimeter | Sum of the perimeters of each hole in the particle. | — | — | |||
| Max Feret Diameter | Distance between the Max Feret Diameter Start and the Max Feret Diameter End. | F |
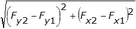
|
|||
| Equivalent Ellipse Major Axis | Length of the major axis of the Equivalent Ellipse. | E2a |

|
|||
| Equivalent Ellipse Minor Axis | Length of the minor axis of the Equivalent Ellipse. | E2b |
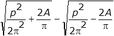
|
|||
| Equivalent Ellipse Minor Axis (Feret) | Length of the minor axis of the ellipse with the same area as the particle, and Major Axis equal in length to the Max Feret Diameter. | EF2b |

|
|||
| Equivalent Rect Long Side | Longest side of the Equivalent Rect. | Ra |

|
|||
| Equivalent Rect Short Side | Shortest side of the Equivalent Rect. | Rb |
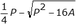
|
|||
| Equivalent Rect Diagonal | Distance between opposite corners of the Equivalent Rect. | Rd |

|
|||
| Equivalent Rect Short Side (Feret) | Shortest side of the rectangle with the same area as the particle, and longest side equal in length to the Max Feret Diameter. | RFb |
 |
|||
| Average Horiz. Segment Length | Average length of a horizontal segment in the particle. Sum of the horizontal segments that do not superimpose any other horizontal segment. Average Horiz. Segment Length is always given as a pixel measurement. | — | A SH |
|||
| Average Vert. Segment Length | Average length of a vertical segment in the particle. Sum of the vertical segments that do not superimpose any other vertical segment. Average Vert. Segment Length is always given as a pixel measurement. | — | A SV |
|||
| Hydraulic Radius | Particle area divided by the particle perimeter. | — | A P |
|||
| Waddel Disk Diameter | Diameter of a disk with the same area as the particle. | — |
|
Ellipses
- Equivalent Ellipse Major Axis—Total length of the major axis of the ellipse that has the same area and same perimeter as a particle. This length is equal to 2a.
This definition gives the following set of equations:
Area = πab
| Perimeter = π | √ | 2(a2 + b2) |
where |
a = 1/2 E2a |
| a = 1/2 E2a |

For a given area and perimeter, only one solution (a, b) exists.
- Equivalent Ellipse Minor Axis—Total length of the minor axis of the ellipse that has the same area and same perimeter as a particle. This length is equal to 2b.
- Ellipse Ratio—Ratio of the major axis of the equivalent ellipse to its minor axis, which is defined as
| ellipse major axis | + | a |
| ellipse minor axis | b |
The more elongated the equivalent ellipse, the higher the ellipse ratio. The closer the equivalent ellipse is to a circle, the closer the ellipse ratio is to 1.
Rectangles
- Equivalent Rect Long Side—Length of the long side (Ra) of the rectangle that has the same area and same perimeter as a particle
This definition gives the following set of equations:
A = Area = RaRb
P = Perimeter = 2(RaRb)

This set of equations can be expressed so that the sum Ra + Rb and the product RaRb become functions of the parameters Particle Area and Particle Perimeter. Ra and Rb then become the two solutions of the following polynomial equation:
2x2 – Px + 2A = 0
Notice that for a given area and perimeter, only one solution (Ra, Rb) exists.
- Equivalent Rect Short Side—Length of the short side of the rectangle that has the same area and same perimeter as a particle. This length is equal to Rb.
- Equivalent Rect Diagonal—Distance between opposite corners of the Equivalent Rect.
| √ | R2a + R2b |
- Rectangle Ratio—Ratio of the long side of the equivalent rectangle to its short side, which is defined as
| rectangle long side | = | Ra |
| rectangle short side | Rb |
The more elongated the equivalent rectangle, the higher the rectangle ratio.
The closer the equivalent rectangle is to a square, the closer to 1 the rectangle ratio.
Hydraulic Radius
A disk with radius R has a hydraulic radius equal to
| disk area disk perimeter |
= | πR2 2πR |
= | R 2 |
Areas
The following table lists the NI Vision particle area measurements.
| Measurement | Definition | Symbol | Equation |
|---|---|---|---|
| Area | Area of the particle. | A | — |
| Area of Hole | Sum of the areas of each hole in the particle. | AH | — |
| Area of Particle & Holes | Area of a particle that completely covers the image. | AT | A + AH |
| Convex Hull Area | Area of the particle Convex Hull. | ACH | — |
| Image Area | Area of the image. | AI | — |
Image Area
Figure A shows an image of a calibration grid. The image exhibits nonlinear distortion. Figure B shows an image of coins taken with the same camera setup used in figure A. The dashed line around figure B defines the image area in pixels. Figure C illustrates the image of coins after image correction. The dashed line around figure C defines the image area in calibrated units.

Quantities
The following table lists the NI Vision particle measurements relating to quantity.
| Measurement | Definition | Symbol |
|---|---|---|
| Number of Holes | Number of holes in the particle. | — |
| Number of Horiz. Segments | Number of horizontal segments in the particle. Number of Horiz. Segments is always given as a pixel measurement. | SH |
| Number of Vert. Segments | Number of vertical segments in the particle. Number of Vert. Segments is always given as a pixel measurement. | SV |
Angles
The following table lists the NI Vision particle angle measurements. The equations are given in radians. The results are given in degrees that are mapped into the range 0 to 180, such that 0 ≤ θ < 180.
| Measurement | Definition | Equation | |||||
|---|---|---|---|---|---|---|---|
| Orientation | The angle of the line that passes through the particle Center of Mass about which the particle has the lowest moment of inertia. |
|
|||||
| Max Feret Diameter Orientation | The angle of the Max Feret Diameter. |
|
The Orientation angle is measured counterclockwise from the horizontal axis, as shown in the following figure. The value can range from 0° to 180°. Angles outside this range are mapped into the range. For example, a 190° angle is considered to be a 10° angle.

|
|
|
1 Line with Lowest Moment of Inertia 2 Orientation in Degrees |
3 Horizontal Axis |
 |
Note Refer to the max feret diameter entry in the for an illustration of Max Feret Diameter Orientation. |
Ratios
The following table lists the NI Vision particle ratio measurements.
| Measurement | Definition | Equation | |||
|---|---|---|---|---|---|
| % Area/Image Area | Percentage of the particle Area covering the Image Area. |
|
|||
| % Area/(Area of Particle & Holes) | Percentage of the particle Area in relation to the Area of its Particle & Holes |
|
|||
| Ratio of Equivalent Ellipse Axes | Equivalent Ellipse Major Axis divided by Equivalent Ellipse Minor Axis. | E2a E2a |
|||
| Ratio of Equivalent Rect Sides | Equivalent Rect Long Side divided by Equivalent Rect Short Side. | Ra Rb |
Factors
The following table lists the NI Vision particle factor measurements.
| Measurement | Definition | Equation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Elongation Factor | Max Feret Diameter divided by Equivalent Rect Short Side (Feret). The more elongated the shape of a particle, the higher its elongation factor. | F RFb |
|||||||||
| Compactness Factor | Area divided by the product of Bounding Rect Width and Bounding Rect Height. The compactness factor belongs to the interval [0, 1]. | A W · H |
|||||||||
| Heywood Circularity Factor | Perimeter divided by the circumference of a circle with the same area. The closer the shape of a particle is to a disk, the closer the Heywood circularity factor is to 1. |
|
|||||||||
| Type Factor | Factor relating area to moment of inertia. |
|
|||||||||
Sums
The following table lists the NI Vision particle sum measurements.
| Measurement | Symbol |
|---|---|
| Sum x | ∑x |
| Sum y | ∑y |
| Sum xx | ∑xx |
| Sum xy | ∑xy |
| Sum yy | ∑yy |
| Sum xxx | ∑xxx |
| Sum xxy | ∑xxy |
| Sum xyy | ∑xyy |
| Sum yyy | ∑yyy |
Moments
The following table lists the NI Vision particle moment measurements.
| Measurement | Symbol | Equation | |||
|---|---|---|---|---|---|
| Moment of Inertia xx | Ixx |
|
|||
| Moment of Inertia xy | Ixy |
|
|||
| Moment of Inertia yy | Iyy |
|
|||
| Moment of Inertia xxx | Ixxx |
∑xxx – 3x∑xx + 2x2∑x |
|||
| Moment of Inertia xxy | Ixxy | ∑xxy – 2x∑xy – y∑xx + 2x2∑y |
|||
| Moment of Inertia xyy | Ixyy | ∑xyy – 2y∑xy – x∑yy + 2y2∑x |
|||
| Moment of Inertia yyy | Iyyy |
∑yyy – 3y∑yy + 2y2∑y |
|||
| Norm. Moment of Inertia xx | Nxx | Ixx A2 |
|||
| Norm. Moment of Inertia xy | Nxy | Ixy A2 |
|||
| Norm. Moment of Inertia yy | Nyy | Iyy A2 |
|||
| Norm. Moment of Inertia xxx | Nxxx | Ixxx A5/2 |
|||
| Norm. Moment of Inertia xxy | Nxxy | Ixxy A5/2 |
|||
| Norm. Moment of Inertia xyy | Nxyy | Ixyy A5/2 |
|||
| Norm. Moment of Inertia yyy | Nyyy | Iyyy A5/2 |
|||
| Hu Moment 1 | H1 | Nxx + Nyy | |||
| Hu Moment 2 | H2 | (Nxx – Nyy)2 + 4Nxy2 | |||
| Hu Moment 3 | H3 | (Nxxx – 3Nxyy)2 + (3Nxxy – Nyyy)2 | |||
| Hu Moment 4 | H4 | (Nxxx + Nxyy)2 + (Nxxy – Nyyy)2 | |||
| Hu Moment 5 | H5 | (Nxxx – 3Nxyy)(Nxxx + 3Nxyy)[(Nxxx + 3Nxyy)2 – 3(Nxxy + 3Nyyy)2] + (3Nxxy – Nyyy)(Nxxy + Nyyy) [(3Nxxx + Nxyy)2 – (3Nxxy + Nyyy)2] |
|||
| Hu Moment 6 | H6 | (Nxx – Nyy)[(Nxxx + Nxyy)2 – (Nxxy + Nyyy)2] + 4Nxy(Nxxx + Nxyy)2 – (Nxxy + Nyyy)] |
|||
| Hu Moment 7 | H7 | (3Nxxy – Nyyy)(Nxxx + Nxyy)[(Nyyy + Nxyy)2 – 3(Nxxy + Nyyy)2] + (3Nxyy – Nyyy)(Nxxy + Nyyy) [3(Nxxx + Nxyy)2 – (Nxxy + Nyyy)2] |