PID (PID)

Implements a single-precision floating-point PID algorithm for PID applications with high-speed control and/or high channel count on an FPGA target. You can use this VI to create single-channel, multi-channel, and multi-rate control applications.

The PID algorithm features control action range and uses an integrator anti-windup calculation to limit the effect of the integral action during transients. The PID algorithm also features bumpless controller output for PID gain changes.


icon

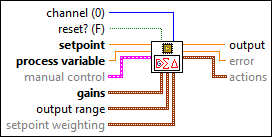
Inputs/Outputs

  • cu8.png channel (0) —

    channel specifies the channel that this VI processes. The valid value range is [0, 255]. The default is 0.

  • cbool.png reset? (F) —

    reset? specifies whether to reset the internal state of the channel that you specify. The default is FALSE.

  • csgl.png setpoint —

    setpoint specifies the value that you want process variable to attain. In equations that define the PID controller, SP represents setpoint.

  • csgl.png process variable —

    process variable specifies the value of the variable that you want to control. In equations that define the PID controller, PV represents process variable.

  • ccclst.png manual control —

    manual control specifies the control mode and the control output value for the manual control mode.

  • cbool.png manual? (F) —

    manual? specifies whether to use the automatic or manual control mode. The default is FALSE, which specifies to use the automatic control mode.

  • csgl.png manual input (0) —

    manual input specifies the control output value for the manual control mode. The default is 0.

  • cnclst.png gains —

    gains specifies the proportional gain, integral gain, derivative gain, and filter coefficient parameters of the controller. The proportional gain, integral gain, and derivative gain are normalized.

    Use the Convert PID Gains VI to convert PID gains into the form that gains requires.

  • csgl.png proportional gain —

    proportional gain specifies the normalized proportional gain of the controller. In equations that define the PID controller, Kp represents proportional gain.

  • csgl.png integral gain —

    integral gain specifies the normalized integral gain of the controller. In equations that define the PID controller, Ki represents integral gain.

  • csgl.png derivative gain —

    derivative gain specifies the normalized derivative gain of the controller. In equations that define the PID controller, Kd represents derivative gain.

  • csgl.png filter coefficient —

    filter coefficient specifies the derivative lowpass filter coefficient of the controller. The valid value range is [0, 1]. Increasing the value of filter coefficient increases damping of the derivative action. In equations that define the PID controller, a represents filter coefficient.

  • cnclst.png output range —

    output range specifies the range for the control output value. If the control output value is outside output range, this VI coerces the value to fall within the range and returns the coerced value as the control output value. This VI implements integrator anti-windup when the control output is saturated at the specified minimum or maximum value.

  • csgl.png output high (Inf) —

    output high specifies the maximum control output value. The default is Inf.

  • csgl.png output low (-Inf) —

    output low specifies the minimum control output value. The default is -Inf.

  • cnclst.png setpoint weighting —

    setpoint weighting specifies corrections to apply to the error values of the controller. setpoint weighting tunes the proportional action and the derivative action.

  • csgl.png proportional weighting (1) —

    proportional weighting specifies the relative emphasis of setpoint tracking to disturbance rejection. The valid value range is [0, 1]. The default is 1, which is appropriate for most applications. In equations that define the PID controller, beta represents proportional weighting.

  • csgl.png derivative weighting (0) —

    derivative weighting specifies an amount by which to weight the error applied to the derivative action. The default value is 0, which avoids the derivative kick. The valid value range is [0, 1]. In equations that define the PID controller, gamma represents derivative weighting.

  • isgl.png output —

    output returns the control output value of the PID algorithm.

  • isgl.png error —

    error returns the difference between setpoint and process variable.

  • inclst.png actions —

    actions returns the values of the proportional action, the integral action, and the derivative action in the PID algorithm.

  • isgl.png proportional action —

    proportional action returns the value of the proportional action.

  • isgl.png integral action —

    integral action returns the value of the integral action.

  • isgl.png derivative action —

    derivative action returns the value of the derivative action.

    • The PID VI calculates the output, u(k), according to the following equations:

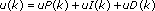
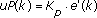
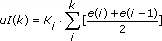
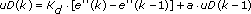
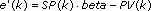
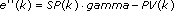
    where

    Kp is proportional gain Ki is integral gain Kd is derivative gain a is filter coefficient SP is setpoint beta is proportional weighting PV is process variable gamma is derivative weighting

    Examples

    Refer to the following example files included with LabVIEW FPGA Module.

    • labview\examples\CompactRIO\FPGA Fundamentals\FPGA Math and Analysis\Floating-point PID\Multi-Channel PID\Multi-Channel PID.lvproj
    • labview\examples\CompactRIO\FPGA Fundamentals\FPGA Math and Analysis\Floating-point PID\Multi-Rate PID\Multi-Rate PID.lvproj
    • labview\examples\R Series\FPGA Fundamentals\FPGA Math and Analysis\Floating-point PID\Multi-Channel PID\Multi-Channel PID.lvproj
    • labview\examples\R Series\FPGA Fundamentals\FPGA Math and Analysis\Floating-point PID\Multi-Rate PID\Multi-Rate PID.lvproj