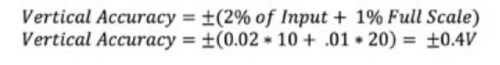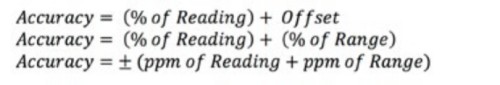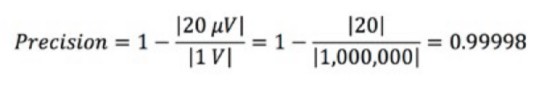Analoge Sample-Qualität: Genauigkeit, Empfindlichkeit, Präzision und Rauschen

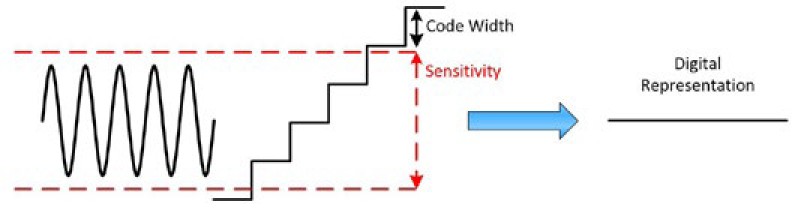
Wenn es um die Sample-Qualität geht, möchten Sie wahrscheinlich die Genauigkeit und Präzision Ihrer Messung beurteilen. Es ist jedoch wichtig, zuerst die Empfindlichkeit Ihres Oszilloskops zu verstehen. Die Empfindlichkeit ist die kleinste Änderung eines Eingangssignals, die zum Ansprechen des Messgeräts führen kann. Wenn sich ein Eingangssignal also um einen bestimmten Wert ändert, d. h. um eine bestimmte Empfindlichkeit, können sich die Digitaldaten ändern.

Verwechseln Sie Empfindlichkeit nicht mit Auflösung und Code-Breite. Die Auflösung bestimmt die Code-Breite. Dies ist der diskrete Pegel, bei dem das Gerät Werte anzeigt. Die Empfindlichkeit definiert jedoch die Spannungsänderung, die das Gerät benötigt, um eine Wertänderung zu registrieren. Ein Gerät mit einem Messbereich von 10 V kann beispielsweise Signale mit einer Auflösung von 1 mV erfassen, die kleinste messbare Spannung kann jedoch 15 mV betragen. In diesem Fall hat das Gerät eine Auflösung von 1 mV, aber eine Empfindlichkeit von 15 mV.

In einigen Fällen ist die Empfindlichkeit größer als die Code-Breite. Dies mag auf den ersten Blick widersprüchlich erscheinen, denn bedeutet das nicht, dass sich die Spannung um einen Wert ändert, der angezeigt, aber nicht registriert werden kann? Ja! Um den Vorteil zu verstehen, stellen Sie sich eine konstante Gleichspannung vor. Obwohl es großartig wäre, wenn diese Spannung ohne Abweichungen wirklich genau konstant wäre, gibt es immer geringfügige Schwankungen in einem Signal, wie in Abbildung 1 dargestellt. Die Empfindlichkeit ist mit roten Linien gekennzeichnet, außerdem wird die Code-Breite dargestellt. Da die Spannung in diesem Beispiel nie den Empfindlichkeitspegel überschreitet, wird sie durch denselben Digitalwert dargestellt, auch wenn er größer als die Code-Breite ist. Dies hat den Vorteil, dass kein Rauschen aufgenommen und das Signal genauer als konstante Spannung dargestellt wird.

^{Abbildung 1: Eine Empfindlichkeit, die größer als die Code-Breite ist, kann dazu beitragen, ein verrauschtes Signal zu glätten.}

Sobald das Signal tatsächlich ansteigt, überschreitet es den Empfindlichkeitspegel und wird dann durch einen anderen Digitalwert dargestellt. Siehe Abbildung 2. Beachten Sie, dass Ihre Messung niemals genauer sein kann als die Empfindlichkeit.

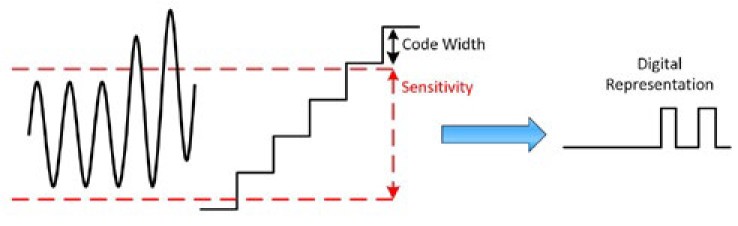
^{Abbildung 2: Sobald das Signal den Empfindlichkeitspegel überschreitet, wird es durch einen anderen Digitalwert dargestellt.}

Es gibt auch einige Unklarheiten bei der Definition der Empfindlichkeit eines Geräts. Manchmal kann sie, wie im obigen Beispiel zu sehen, als konstante Menge definiert werden. In diesem Fall wird das Signal durch einen anderen Digitalwert dargestellt, sobald das Eingangssignal den Empfindlichkeitspegel überschreitet. Manchmal wird die Empfindlichkeit jedoch auch als Signaländerung definiert. Nachdem sich das Signal um den angegebenen Empfindlichkeitswert geändert hat, wird sie durch ein anderes Signal dargestellt. In diesem Fall kommt es nicht auf die absolute Spannung an, sondern auf die Spannungsänderung. Darüber hinaus definieren einige Geräte die Empfindlichkeit als ungefähr null. 

Dabei ist anzumerken: Nicht nur, dass die genaue Definition der „Empfindlichkeit“ von Unternehmen zu Unternehmen unterschiedlich ist, sondern auch für verschiedene Produkte desselben Unternehmens eine etwas andere Bedeutung haben kann. Es ist wichtig, dass Sie die Spezifikationen Ihres Geräts überprüfen, um zu sehen, wie die Empfindlichkeit definiert ist; Wenn die Dokumentation nicht ausreichend ist, wenden Sie sich zur Klärung an das Unternehmen.

Genauigkeit ist ein Maß für die Fähigkeit eines Geräts, den Wert eines gemessenen Signals richtig anzuzeigen. Dieser Begriff hat nichts mit der Auflösung zu tun. Die Genauigkeit kann jedoch nie besser sein als die Auflösung des Geräts.

Je nach Gerät oder Digitizer werden unterschiedliche Anforderungen an die Genauigkeit gestellt. Im Allgemeinen wird von einem Digitalmultimeter (DMM) beispielsweise eine höhere Genauigkeit als von einem Oszilloskop erwartet. Wie die Genauigkeit berechnet wird, variiert ebenfalls je nach Gerät. Überprüfen Sie immer die Spezifikationen Ihres Geräts, um zu erfahren, wie die Genauigkeit von Ihrem Gerät berechnet wird. 

Genauigkeit eines Oszilloskops

Oszilloskope definieren die Genauigkeit des horizontalen und vertikalen Systems getrennt. Das horizontale System bezieht sich auf die Zeitskala oder die X-Achse; die horizontale Systemgenauigkeit ist die Genauigkeit der Zeitbasis. Das vertikale System ist die gemessene Spannung oder die Y-Achse. Die vertikale Systemgenauigkeit ist die Verstärkungs- und Offset-Genauigkeit. Normalerweise ist die vertikale Systemgenauigkeit wichtiger als die horizontale.

Die vertikale Genauigkeit wird normalerweise als Prozentsatz des Eingangssignals und als Prozentsatz des Skalenendwerts angegeben. Einige Spezifikationen unterteilen das Eingangssignal in vertikale Verstärkungs- und Offset-Genauigkeit. Gleichung 1 zeigt zwei verschiedene Möglichkeiten, wie die definierte Genauigkeit angezeigt werden kann. 

^{Gleichung 1: Berechnen der vertikalen Genauigkeit eines Oszilloskops.}

Ein Oszilloskop kann beispielsweise die vertikale Genauigkeit wie folgt bestimmen: 

Bei einem 10-V-Eingangssignal und unter Verwendung des 20-V-Bereichs können Sie die Genauigkeit berechnen: 

Genauigkeit von Digitalmultimeter (DMM) und Netzteil

Digitalmultimeter und Netzteile geben die Genauigkeit normalerweise als Prozentsatz des Messwerts an. Gleichung 2 zeigt drei verschiedene Möglichkeiten, die Genauigkeit eines Digitalmultimeters oder Netzteils auszudrücken.

^{Gleichung 2: Berechnung der vertikalen Genauigkeit eines Digitalmultimeters oder Netzteils.}

Der Begriff „ppm“ bedeutet „Teile pro Million“ (parts per million). Für die meisten Spezifikationen gibt es mehrere Tabellen zur Bestimmung der Genauigkeit. Die Genauigkeit hängt von der Art der Messung, dem Bereich und der Zeit seit der letzten Kalibrierung ab. Überprüfen Sie Ihre Spezifikationen, um zu sehen, wie die Genauigkeit berechnet wird. 

Ein Digitalmultimeter ist beispielsweise auf den 10-V-Bereich eingestellt, arbeitet 90 Tage nach der Kalibrierung bei 23 °C ± 5 °C und erwartet ein 7-V-Signal. Die Genauigkeitsspezifikationen für diese Bedingungen lauten ± (20 ppm des Messwerts + 6 ppm des Bereichs). Sie können dann die Genauigkeit berechnen:

In diesem Fall sollte der Messwert innerhalb von 200 μV der tatsächlichen Eingangsspannung liegen.  

Genauigkeit eines DAQ-Geräts

DAQ-Karten definieren Genauigkeit oft als Abweichung von einer idealen Übertragungsfunktion. Gleichung 3 zeigt ein Beispiel dafür, wie eine DAQ-Karte die Genauigkeit angeben könnte.

^{Gleichung 3: Berechnen der Genauigkeit eines DAQ-Geräts.}

Anschließend werden die einzelnen Terme definiert: 

Die meisten dieser Terme sind tabellarisch definiert und basieren auf dem Nennbereich. Die Spezifikationen legen auch die Berechnung der Rauschunsicherheit fest. Die Rauschunsicherheit ist die Unsicherheit der Messung aufgrund des Einflusses von Rauschen auf die Messung und wird bei der Bestimmung der Genauigkeit berücksichtigt.

Darüber hinaus gibt es möglicherweise mehrere Genauigkeitstabellen für Ihr Gerät, je nachdem, ob Sie die Genauigkeit von Analogeingang oder Analogausgang ermitteln möchten oder ob ein Filter aktiviert oder deaktiviert ist.

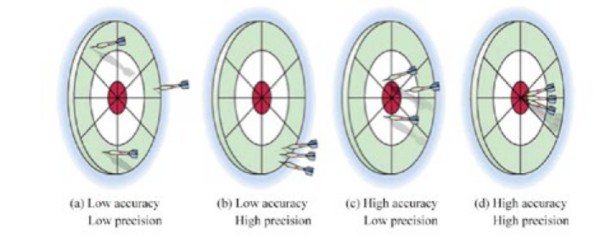
Genauigkeit und Präzision werden oft synonym verwendet, aber es gibt einen feinen Unterschied. Die Genauigkeit ist definiert als Maß für die Stabilität des Geräts und seine Fähigkeit, mit demselben Eingangssignal immer wieder den gleichen Messwert zu erzielen. Während sich die Genauigkeit darauf bezieht, wie nahe ein gemessener Wert am tatsächlichen Wert liegt, bezieht sich die Präzision darauf, wie genau einzelne, wiederholte Messungen miteinander übereinstimmen. 

^{Abbildung 3: Präzision und Genauigkeit hängen zusammen, sind aber nicht dasselbe.}

Die Präzision wird am stärksten durch Rauschen und kurzzeitige Drifts des Geräts beeinflusst. Die Präzision eines Geräts wird oft nicht direkt angegeben, sondern muss aus anderen Spezifikationen wie dem Übertragungsverhältnis, dem Rauschen und dem Temperaturdrift abgeleitet werden. Wenn Sie über eine Reihe von Messungen verfügen, können Sie die Präzision berechnen.

^{Gleichung 4: Berechnung der Präzision.}

Wenn Sie beispielsweise eine konstante Spannung von 1 V überwachen und feststellen, dass sich Ihr Messwert zwischen den Messungen um 20 µV ändert, kann Ihre Messpräzision wie folgt berechnet werden: 

In der Regel wird die Präzision in Prozent angegeben. In diesem Beispiel beträgt die Präzision 99,998 Prozent.

Die Präzision ist vor allem dann von Bedeutung, wenn relative Messungen (im Vergleich zu einem vorherigen Messwert desselben Werts), z. B. bei der Gerätekalibrierung, durchgeführt werden müssen.

Verwechseln Sie Empfindlichkeit nicht mit Auflösung und Code-Breite. Die Auflösung bestimmt die Code-Breite. Dies ist der diskrete Pegel, bei dem das Gerät Werte anzeigt. Die Empfindlichkeit definiert jedoch die Spannungsänderung, die das Gerät benötigt, um eine Wertänderung zu registrieren. Ein Gerät mit einem Messbereich von 10 V kann beispielsweise Signale mit einer Auflösung von 1 mV erfassen, die kleinste messbare Spannung kann jedoch 15 mV betragen. In diesem Fall hat das Gerät eine Auflösung von 1 mV, aber eine Empfindlichkeit von 15 mV.

Thermisches Rauschen

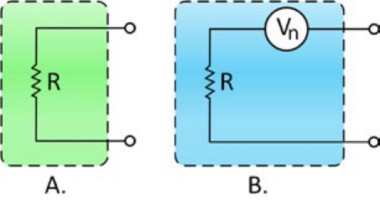
Ein idealer elektronischer Schaltplan erzeugt kein eigenes Rauschen, daher enthält das Ausgangssignal des idealen Schaltplans nur das Rauschen des ursprünglichen Signals. Reale elektronische Schaltpläne und Komponenten erzeugen jedoch ein gewisses Eigenrauschen. Selbst der einfache Festwertwiderstand ist verrauscht. 

^{Abbildung 4: Ein idealer Widerstand spiegelt sich in A wider, aber praktisch haben Widerstände ein internes thermisches Rauschen, wie in B dargestellt.}

Die Abbildung 4A zeigt den Ersatzschaltplan für einen idealen, rauschfreien Widerstand. Das Eigenrauschen wird in Abbildung 4B durch eine Rauschspannungsquelle Vn in Reihe mit dem idealen, rauschfreien Widerstand Ri dargestellt. Bei jeder Temperatur über der absoluten Nullstelle (0 °K oder etwa -273 °C) befinden sich Elektronen in jedem Material in ständiger zufälliger Bewegung. Aufgrund der inhärenten Zufälligkeit dieser Bewegung fließt jedoch kein Strom in eine Richtung. Mit anderen Worten, der Elektronendrift in eine beliebige Richtung wird über kurze Zeiträume durch den gleichen Drift in die entgegengesetzte Richtung aufgehoben. Elektronenbewegungen sind daher statistisch dekorreliert. Im Material wird jedoch eine kontinuierliche Folge zufälliger Stromimpulse erzeugt, die von der Außenwelt als Störsignal wahrgenommen werden. Dieses Signal hat mehrere Namen: Johnson-Rauschen, Wärmerauschen oder thermisches Rauschen. Dieses Rauschen nimmt mit der Temperatur und dem Widerstand zu, aber als Quadratwurzelfunktion. Das bedeutet, dass Sie den Widerstand vervierfachen müssen, um das Rauschen dieses Widerstands zu verdoppeln.

Funkelrauschen oder ¹/_F-Rauschen 

Halbleiterbauelemente neigen dazu, ein Rauschen aufzuweisen, das nicht flach mit der Frequenz verläuft. Es steigt am unteren Ende an. Es wird als ¹/_F-Rauschen, rosa Rauschen, übermäßiges Rauschen oder Funkelrauschen bezeichnet. Diese Art von Rauschen tritt auch in vielen anderen physikalischen Systemen abgesehen von elektrischen Systemen auf. Beispiele sind Proteine, Reaktionszeiten kognitiver Prozesse oder sogar Erdbeben. Das folgende Diagramm zeigt die wahrscheinlichste Quelle des Rauschens in Abhängigkeit von der Frequenz, bei der das Rauschen bei einer bestimmten Spannung auftritt. Die Kenntnis der Ursache des Rauschens trägt wesentlich zur Reduzierung des Rauschens bei.

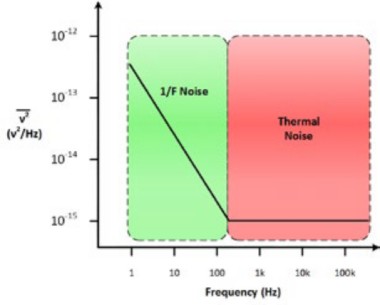
^{Abbildung 4: Ein idealer Widerstand spiegelt sich in A wider, aber praktisch haben Widerstände ein internes thermisches Rauschen, wie in B dargestellt.}

Obwohl Rauschen für Entwickler ein ernstes Problem darstellt, insbesondere bei niedrigen Signalpegeln, können die Auswirkungen von Rauschen auf ein System durch eine Reihe von vernünftigen Ansätzen minimiert werden. Hier sind einige Strategien zur Reduzierung von Rauschen:

• Halten Sie den Quellwiderstand und den Eingangswiderstand des Verstärkers so niedrig wie möglich. Die Verwendung von Widerständen mit hohem Wert erhöht das thermische Rauschen proportional.
• Das thermische Gesamtrauschen ist auch eine Funktion der Bandbreite des Schaltplans. Daher wird auch das Rauschen minimiert, wenn die Bandbreite des Schaltplans auf ein Minimum reduziert wird. Dieser Auftrag muss jedoch sorgfältig durchgeführt werden, da Signale ein Fourier-Spektrum haben, das für eine genaue Messung erhalten bleiben muss. Die Lösung besteht darin, die Bandbreite an den für das Eingangssignal erforderlichen Frequenzgang anzupassen.
• Verhindern Sie, dass externe Störungen die Leistung des Systems beeinträchtigen, indem Maßnahmen wie Erdung, Abschirmung, Verkabelung, sorgfältige Platzierung der Drähte und Filter eingesetzt werden.
• Verwenden Sie in der Eingangsstufe des Systems einen rauscharmen Verstärker.
• Verwenden Sie für einige Halbleiterschaltkreise die niedrigste Gleichstromversorgung, die für diesen Auftrag geeignet ist.

• Die Empfindlichkeit ist die kleinste Änderung eines Eingangssignals, die zum Ansprechen des Messgeräts führt.
• Genauigkeit ist ein Maß für die Fähigkeit eines Geräts, den Wert eines gemessenen Signals richtig anzuzeigen.
• Die Genauigkeit und Empfindlichkeit sind im Spezifikationsdokument erläutert. Da Unternehmen und Produkte desselben Unternehmens diese Begriffe möglicherweise unterschiedlich verwenden, lesen Sie immer die Dokumentation und wenden Sie sich bei Bedarf an das Unternehmen.
• Die Genauigkeit ist definiert als Maß für die Stabilität des Geräts und seine Fähigkeit, mit demselben Eingangssignal immer wieder den gleichen Messwert zu erzielen.
• Rauschen ist jedes unerwünschte Signal, das das gewünschte Signal stört.
• Es gibt verschiedene Arten von Rauschen und verschiedene Strategien zur Reduzierung des Rauschens.

• Erfahren Sie mehr über Erdungstechnologien zur Reduzierung von Rauschen
• Funktionsweise von Antialiasing-Filtern
• Erfahren Sie mehr über NI PXI Digitalmultimeter, Oszilloskope und DAQ-Geräte für die automatisierte Charakterisierung, Validierung und Produktionsprüfung
• Alle Inhalte zu Messgerätegrundlagen herunterladen
• Unterschiede zwischen Genauigkeit, Code-Breite und Auflösungs-Bits