PIDコントローラとそのD理論解説

PIDコントローラは、センサからの入力データを受け取り、実際値と目標値との差を計算し、温度、流量、速度、圧力、電圧などの制御変数に合わせて出力を調整する計測器です。これには、現在の誤差に対応する比例制御、過去の蓄積された誤差に対応する積分制御、将来の誤差を予測する微分制御の3つのメカニズムがあります。PIDコントローラはこれら3つの要素を総合して出力を計算します。このアーキテクチャにより、PIDコントローラはプロセス制御とシステムの安定性を効率的に維持できます。 PIDコントローラのパラメータを定義する前に、閉ループシステムとは何か、またそれに関連するいくつかの用語について説明します。

閉ループシステム

通常、制御システムにおいて、プロセス変数は温度（℃）や圧力（psi）、フローレート（リットル/分）など、制御する必要があるシステムのパラメータとなります。センサがこのプロセス変数を測定し、制御システムにフィードバックを提供します。設定ポイントとは、このプロセス変数の期待値もしくはコマンド値のことです。例えば、温度制御システムで言えば、摂氏100℃などが設定ポイントです。常に、プロセス変数と設定ポイントの差は制御システムのアルゴリズム(補償器)に使用され、これによってシステム（プラント）を駆動するためのアクチュエータの出力が決まります。例えば、計測した温度のプロセス変数が100℃で、期待する温度設定ポイントが120℃であるとします。この場合には、制御アルゴリズムが指定したアクチュエータ出力によりヒーターを駆動するはずです。アクチュエータを駆動することによりヒーターがオンになると、システムは暖かくなり、その結果、温度プロセス変数は増加します。これは、一定のフィードバックを行うセンサの読み取りと、期待するアクチュエータ出力の計算というプロセスが連続して繰り返されるため、閉ループ制御システムと呼ばれます。図1は一定のループレートです。

多くの場合、アクチュエータの出力は、システムに影響を及ぼす信号とは限りません。例えば、恒温槽には冷気の供給源があり、チェンバの中に冷気が吹き込んで温度を乱すことがあります。これを外乱といいます。弊社では、プロセス変数に対する外乱の影響を最小限に抑える制御システムの設計に努めています。

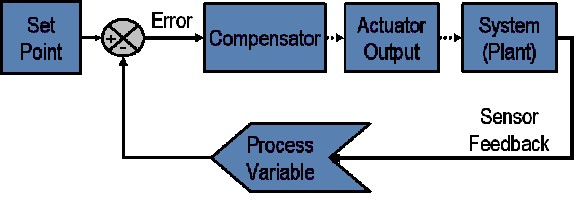
^{図1:一般的な閉ループシステムのブロック図}

用語の定義

制御システムを設計する工程においては、まず、性能の要件を定義します。制御システムの性能は、ステップ関数を設定値のコマンド変数として適用し、プロセス変数の応答を計測することで測定します。一般的に、応答は定義された波形特性を計測することで定量化されます。立ち上がり時間とは、システムの定常状態もしくは最終値の10～90％に達するために要する時間のことです。パーセントオーバーシュートとは、プロセス変数が最終値をオーバーシュートする分量であり、最終値をパーセントで示したものです）。整定時間とは、プロセス変数が最終値のある一定の割合（通常5％）以内で整定するのに必要な時間のことです。定常状態エラーとは、プロセス変数と設定値の最終的な差のことです。以上の定義は、工業分野や学問分野によって呼び方が変わりますので、ご注意ください。

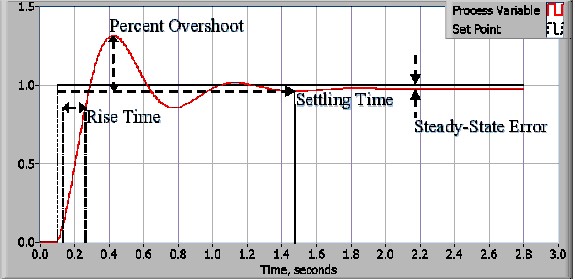
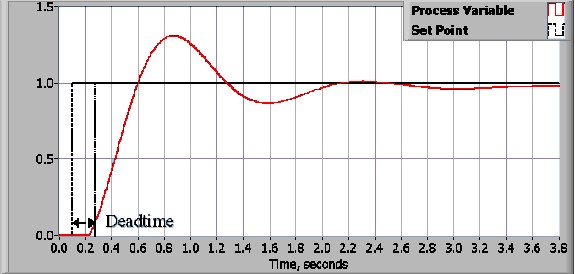
性能要件を指定したら、次はシステムを検査し、適切な制御スキームを選択します。このPID制御により、非常に多くのアプリケーションが成功を収めています。

比例応答

比例コンポーネントは、設定ポイントとプロセス変数の差にのみ依存します。この差は誤差項と呼ばれます。エラー信号への出力応答の速度は、比例ゲイン （K_c）により決定されます。例えば、誤差項の振幅が10の場合、比例ゲイン５は50の比例応答を生成します。一般に、比例ゲインが大きいほど、制御システムの応答速度は高くなります。ただし、比例ゲインが大きすぎるとプロセス変数は変動し始めます。K_cがさらに大きくなるにつれて変動も大きくなり、システムは不安定な状態となり、場合によっては制御不可能となる可能性があります。

積分応答

積分成分は長時間に渡って発生した誤差項を蓄積します。つまり、小さい誤差項でも、積分成分は少しずつ増加していきます。積分応答は、エラーがゼロでない限り時間の経過に伴い増加し続けるため、定常状態エラーをゼロにする効果があります。定常状態エラーとは、プロセス変数と設定値の最終的な差のことです。コントローラがエラー信号をゼロに駆動せずに積分動作によりコントローラが飽和状態となると、積分ワインドアップと呼ばれる現象が生じます。

微分応答

プロセス変数が急激に増加すると、微分成分のために出力が低下します。微分応答はプロセス変数が変化する速度に比例します。微分時間（T_d）パラメータを増加すると、制御システムは誤差項の変化に対して大きく反応し、制御システム応答の速度は全体的に向上します。微分制御はプロセス変数信号のノイズに対して影響を受けやすいため、通常、ほとんどの実際の制御システムにおいては非常に短い微分時間（T_d）を使用します。センサのフィードバック信号のノイズが大きい場合もしくは制御ループ速度が非常に遅い場合には、微分応答により制御システムは不安定になる可能性があります。

P (比例)・I (積分)・D (微分) が制御システムから理想的な応答を得るためにゲインを最適化するプロセスを、チューニングといいます。 PIDチューニングには様々なメソッドがあります。「Guess and Check」メソッドと「Ziegler Nichols」メソッドについて後ほどご説明します。

PIDコントローラのゲインはトライアル&エラーメソッドにより得られます。エンジニアが各ゲインパラメータの重要性を理解すれば、このメソッドは比較的簡単です。このメソッドでは、まずIとDがゼロに設定され、ループ出力が変動するまで比例ゲインが向上します。比例ゲインを向上させるとシステムは高速になりますが、システムが不安定な状態にならないよう対策が必要となります。Pが希望の応答速度となるよう設定されると、積分項が増加して変動は停止します。積分項により定常状態との誤差は減少しますが、オーバーシュートは増加します。ある程度のオーバーシュートは常に高速なシステムに必要なため、即座に変化に反応する可能性があります。統合項は微調整され、定常状態との誤差を最小限に抑えられます。定常状態との誤差を最小限に抑えた最適な高速制御システムとなるようPとIが設定されると、ループが容認できる程度の高速で設定点に戻るまで微分パラメータが増加し続けます。微分パラメータが増加するとオーバーシュートが減少し、安定性のある高ゲインとなりますが、システムはノイズの影響を非常に受けやすくなります。制御システムにおいては、エンジニアはアプリケーションニーズへの対応を考慮し、一つの特性を得る代わりにもうひとつの特性を妥協するといったことがよく行われます。

Ziegler-Nicholsメソッドも、広く普及したPIDコントローラチューニングメソッドです。これは、IとDがゼロに設定され、ループの変動開始までPが増加する点において、トライアル&エラーメソッドと似ています。変動が開始されると、臨海ゲインK_cと変動周期P_cが記録されます。P、I、Dは、以下の表の列に従って調整されます。

LabVIEW PIDツールセットは、PIDベースの制御システムの設計に非常に役立つ広範なVIを搭載しています。制御出力範囲制限、積分器アンチワインドアップ、PIDゲインの変化に対するコントローラ出力のバンプレスなどが、PID VIの主な機能です。PID Advanced VIには、非線形積分といったPID VIの様々な機能と自由度制御、誤差二乗制御の2つが含まれています。

^{図5:LabVIEW PID制御パレットのVI}

PIDパレットも、PID Autotuning VIやPID Gain Schedule VIなどの上級VIをいくつか装備しています。PID Autotuning VIは、制御システムのPIDのパラメータを再調整する際に役立ちます。P、I、Dの値が知識に基づいた推測がおこなわれると、PID Autotuning VIはPIDのパラメータを再調整し、制御システムからより良い応答が得られます。

制御システムの信頼性は、リアルタイムターゲットで実行するLabVIEW Real Timeモジュールを使用することで大幅に向上します。NIでは、データ集録デバイスを提供しています。データ集録デバイスは、一般的な制御システムよりも高い確度と性能を提供します。

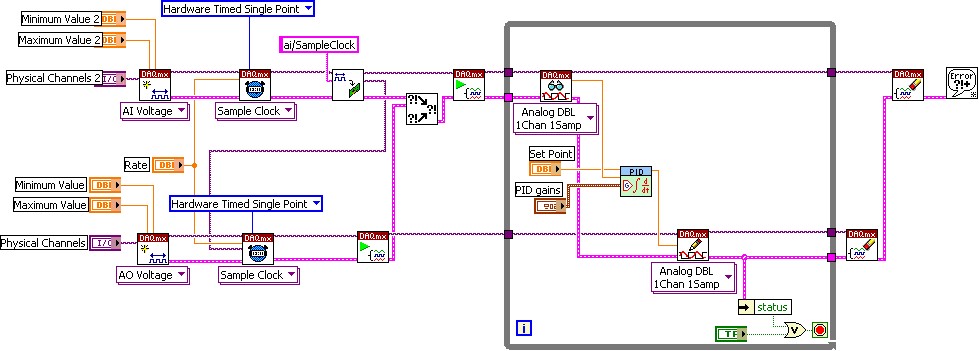
^{図7:プラグインNIデータ収集デバイスを使用してPID制御を行っている一般的なLabVIEW VI}

これらのデータ収集デバイスをLabVIEWと緊密に統合することにより、開発時間を短縮し、エンジニアの生産性を大幅に向上させます。図7は、NIデータ集録ハードウェアに含まれているNI-DAQmxドライバAPIを使用したPID制御を示すLabVIEWの典型的なVIを示しています。

PID制御アルゴリズムは、業界で広く使用されている堅牢でシンプルなアルゴリズムです。このアルゴリズムは十分な柔軟性を備えており、広範なアプリケーションに対して成功をもたらしてきたため、長年に渡り使用され続けています。弊社のNI LabVIEWおよびNIプラグインデータ集録デバイスは、優れたPID制御システムを構築するための高確度および性能の向上をもたらします。

1.Classical PID Control
by Graham C. Goodwin, Stefan F. Graebe, Mario E. Salgado
Control System Design, Prentice Hall PTR

2.PID Control of Continuous Processes
by John W. Webb Ronald A. Reis
Programmable Logic Controllers, Fourth Edition, Prentice Hall PTR