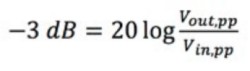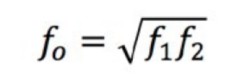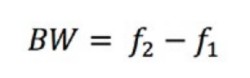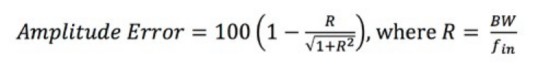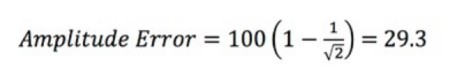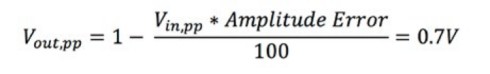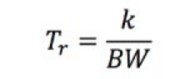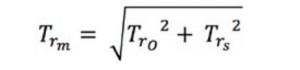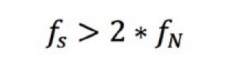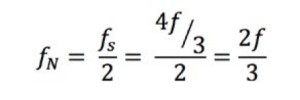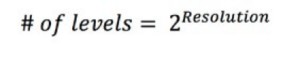アナログ信号の集録:帯域幅、ナイキストサンプリング理論、およびエイリアシング

科学者やエンジニアは多くの場合、デジタイザを使用して実世界のアナログデータをキャプチャし、デジタル信号に変換してから解析を行っています。デジタイザとは、アナログ信号からデジタル信号への変換に使用するデバイスを指します。最も一般的なデジタイザの1つに携帯電話があります。携帯電話では、音声、つまりアナログ信号をデジタル信号に変換して別の電話機に送信します。ただし、テストや測定の用途では、デジタイザといえばオシロスコープまたはデジタルマルチメータ (DMM) を指すことがほとんどです。このドキュメントはオシロスコープに重点を置いていますが、ほとんどのトピックは他のデジタイザにも応用できるものです。

タイプを問わず、システムで波形を正確に再現するにはデジタイザが不可欠です。用途に適したオシロスコープを選定するには、オシロスコープの帯域幅、サンプリングレート、分解能を考慮する必要があります。 

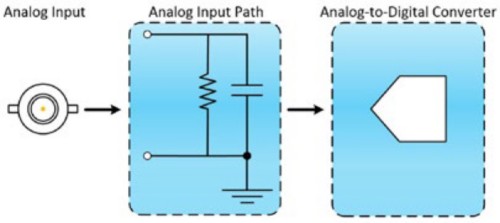
オシロスコープのフロントエンドは、アナログ入力パスとA/D変換器 (ADC) の2つのコンポーネントで構成されています。アナログ入力パスでは、ADCによるデジタル化に備えて信号を最適化するために、信号の減衰、増幅、フィルタ、結合などが行われます。ADCは、信号調節済みのアナログ波形をサンプリングし、アナログ入力波形を表すデジタル値の信号に変換します。入力パスの周波数応答では、振幅および位相の情報が必ず失われます。

帯域幅とは、外界からADCに (すなわちプローブやテストフィクスチャのチップからADCの入力に)、振幅の損失を最小限に抑えながら信号を取り込むアナログフロントエンドの能力を表します。つまり、帯域幅はオシロスコープで正確に測定可能な周波数の範囲を表します。

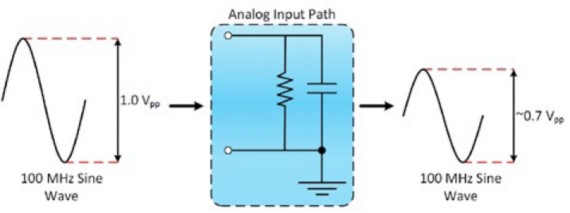
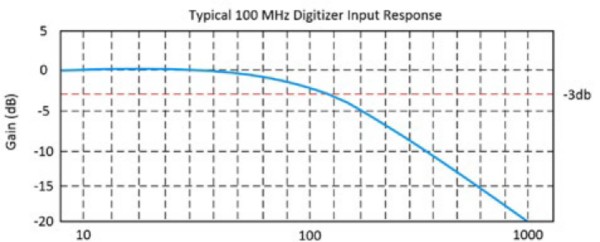
帯域幅は、正弦波入力信号が本来の振幅の70.7%に減衰する周波数と定義され、-3 dBポイントとしても知られています。図2および図3に、100 MHzオシロスコープの一般的な入力応答を示します。

^{図1: 帯域幅は入力信号がオシロスコープのフロントエンドを通過できる周波数範囲を表す。フロントエンドはアナログ入力パスとADCの2つのコンポーネントで構成される}

^{図2:帯域幅とは入力信号が本来の振幅の70.7%に減衰する時点である}

^{図3:このグラフは入力信号が100 MHzで-3 dBポイントに達したことを示す}

帯域幅は、信号振幅がパスバンド周波数よりも3 dB低くなる上限周波数ポイントと下限周波数ポイントの差を測定したものです。複雑に感じますが、分解して考えると、実際は比較的簡単です。 

まず、-3 dB値を計算する必要があります。

^{式1:-3 dBポイントの計算}

V_in,ppは入力信号のピーク-ピーク電圧、V_out,ppは出力信号のピーク-ピーク電圧です。たとえば、式1に示す公式を適用すると、V_out,ppは0.7 Vに近似します。

入力信号が正弦波であるため、出力信号がこの電圧に達する周波数は2つあります。これらをコーナー周波数f₁、f₂と呼びます。これら2つの周波数は、コーナー周波数、カットオフ周波数、交差周波数、電力半値周波数、3 dB周波数、折点周波数など、さまざまな名前で呼ばれます。ただし、これらすべての用語は同じ周波数を表します。信号の中心周波数のf₀はf₁とf₂の幾何平均です。

^{式2:中心周波数の計算}

2つのコーナー周波数の差を計算することで、帯域幅 (BW) を求めることができます。 

^{式3:帯域幅の計算}

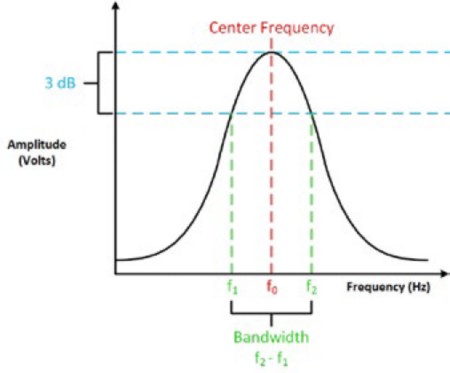
^{図4:帯域幅、コーナー周波数、中心周波数、3 dBポイントはすべてつながっている}

振幅誤差を計算する

多くの場合に役立つもう1つの方程式として、振幅誤差の計算があります。  

^{式4:振幅誤差の計算}

振幅誤差はパーセンテージで表され、Rはオシロスコープの帯域幅 (BW) と入力信号周波数 (f_in) の比率です。

上記の例では、100 MHzオシロスコープに100 MHzの正弦波入力信号を1 Vで与えた場合を考えます。ここで、BW = 100 MHz、(f_in) = 100 MHzです。つまり、R = 1となるため、必要なことは次の方程式を解くのみです。

振幅誤差は29.3%です。次に、1 V信号の出力電圧を特定できます。

振幅誤差を最小限に抑えながら信号をキャプチャするには、オシロスコープの帯域幅を測定信号の最高周波数成分の3～5倍にすることを推奨します。たとえば、1 Vの100 MHz正弦波を正確にキャプチャするには、300～500 MHzの帯域幅のオシロスコープを使用する必要があります。これらの帯域幅での100 MHz信号の振幅誤差は以下のようになります。

立ち上がり時間の計算

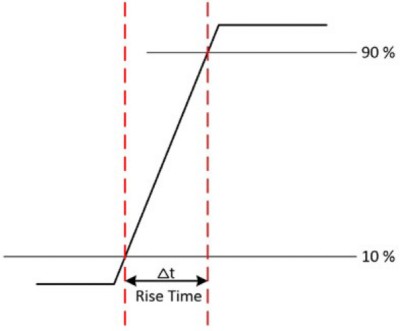
信号を正確に測定するにはオシロスコープに適切な帯域幅が必要ですが、急速な遷移の詳細を正確にキャプチャするには十分な立ち上がり時間も必要です。これは、パルスやステップなどのデジタル信号を測定する場合に最も当てはまります。入力信号の立ち上がり時間は、最大信号振幅の10%から90%に信号が遷移するまでの時間です。20%から80%を使用するオシロスコープもあります。詳細は、必ずユーザマニュアルで確認してください。

^{図5:入力信号の立ち上がり時間は、最大信号振幅の10%から90%に信号が遷移するまでの時間である}

立ち上がり時間 (Tr) は、以下のように求められます。

^{式5:立ち上がり時間の計算}

定数kはオシロスコープによって異なります。帯域幅 (BW) が1 GHz未満のほとんどのオシロスコープは一般的にk = 0.35を示します。一方、帯域幅が1 GHzを超えるオシロスコープのkの値は通常0.4～0.45です。

理論上の立ち上がり時間T_r-mは、オシロスコープの立ち上がり時間T_r-oと入力信号の実際の立ち上がり時間T_r-sに基づき、次の式を使用して計算できます。

^{式6:測定された理論上の立ち上がり時間の計算}

立ち上がり時間の誤差を最小限に抑えながら信号をキャプチャするには、オシロスコープの立ち上がり時間を測定信号の立ち上がり時間の1/3～1/5にすることを推奨します。

サンプリングレートは、帯域幅の仕様とは直接関連していません。サンプリングレートとは、ADCでアナログ入力波形がデジタルデータに変換される周波数のことです。オシロスコープは、アナログ入力パスで信号の減衰、ゲイン、フィルタなどが行われた後、その信号をサンプリングし、結果として得られた波形をデジタル表現に変換します。この変換は、映画のフレームのようなスナップショット単位で行われます。オシロスコープのサンプリングレートが高いほど、波形の解像度が高くなり、詳細な情報が得られます。 

ナイキストサンプリング理論

ナイキストサンプリング理論は、サンプリングレートと測定信号の周波数の関係を説明するものです。この理論では、サンプリングレートf_sは測定信号の対象となる最高周波数成分の2倍以上でなければならないとされています。多くの場合、この周波数はナイキスト周波数、f_Nと呼ばれます。 

^{式7:サンプリングレートはナイキスト周波数の2倍以上でなければならない}

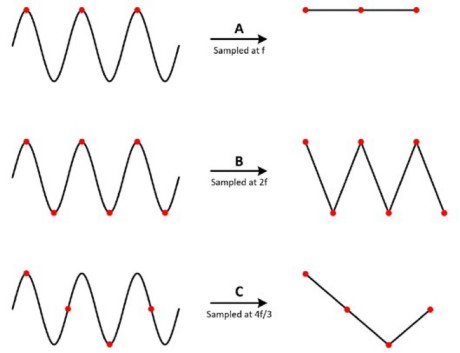
この理由を理解するために、さまざまなレートで測定された正弦波を検討してみましょう。ケースAでは、周波数fの正弦波が、同じ周波数でサンプリングされています。左側の元の信号にはこれらのサンプリング点がマークされており、右側ではこれらのサンプリング点を基に再現された信号が、誤って一定のDC電圧として表示されています。ケースBでは、サンプリングレートは信号の周波数の2倍であり、三角波形として表示されています。この場合、fはナイキスト周波数、つまり所定のサンプリング周波数のエイリアシングを回避する上での周波数成分の上限と等しくなっています。ケースCでは、サンプリングレートは4f/3です。この場合のナイキスト周波数は次のようになります。

このサンプリングレートでは、fがナイキスト周波数よりも大きいことにより、不正確な周波数と形状のエイリアス波形が再現されます。

したがって、波形を正確に再現するには、サンプリングレートfsが測定信号の対象となる最高周波数成分の2倍以上でなければなりません。通常、信号周波数の約5倍以上のサンプリングレートが必要です。

^{図6:サンプリングレートが低すぎると、不正確な波形が再現される可能性がある}

エイリアシング

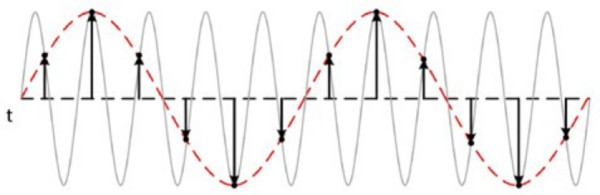
エイリアシングを回避するために特定のレートでサンプリングする必要がある場合があります。それでは、エイリアシングとはどのような状態を指すでしょうか。ナイキスト周波数の2倍よりも低いサンプリングレートで信号をサンプリングすると、そのサンプリングデータには誤った低周波数成分が現れます。この現象をエイリアシングと呼びます。以下の図に、1 MS/sでサンプリングされた800 kHzの正弦波を示します。点線は、上記のサンプリングレートで記録されたエイリアス信号を示します。800 kHzの周波数はエイリアス信号としてパスバンドに入り、誤って200 kHzの正弦波として表示されます。

^{図7:サンプリングレートが低すぎるとエイリアシングが発生し、不正確な波形表現が再現される}

エイリアス周波数f_aを計算し、ナイキスト周波数を超える周波数の入力信号がどのように現れるかを特定することができます。これはサンプリング周波数の整数倍のうち、入力信号の周波数に最も近い整数倍から、入力信号の周波数を減算した絶対値です。 

^{式8:エイリアス周波数の計算}

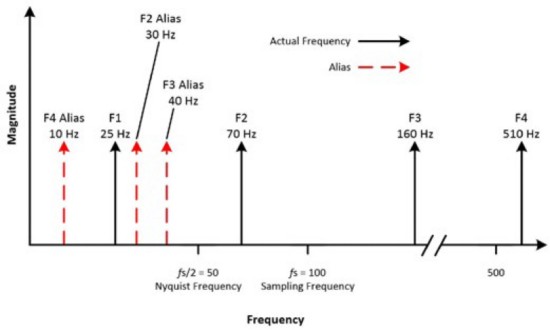
たとえば、サンプリング周波数100 Hzの信号があり、入力信号に25 Hz、70 Hz、160 Hz、510 Hzの周波数が含まれているとします。50 Hzのナイキスト周波数未満の周波数は正確にサンプリングされますが、50 Hzを超える周波数はエイリアスとして現れます。 

^{図8:さまざまな周波数値が測定され、一部はエイリアス周波数であり、残りは波形の実際の周波数である}

以下にエイリアス周波数の計算を示します。 

サンプリングレートを引き上げる以外に、アンチエイリアスフィルタを使用する方法でもエイリアシングを回避できます。アンチエイリアスフィルタとは、入力信号における周波数のうち、ナイキスト周波数よりも大きな周波数を減衰するローパスフィルタです。ADCのサンプリング基準を満たすように入力信号の帯域幅を制限するためには、このフィルタをADCの前段に設置する必要があります。アナログ入力チャンネルでは、エイリアシングを回避するために、ハードウェアにアナログフィルタとデジタルフィルタの両方を実装できます。

特定用途でオシロスコープを選択するときに考慮すべきもう1つの要因は分解能です。分解能のビット数は、オシロスコープで信号の表現に使用可能な垂直レベルの数です。分解能の概念は物差しに例えると理解しやすくなります。1メートルの物差しをミリメートル単位に分割するとします。この場合、分解能とは何を指すでしょうか。分解能は物差しの最小「目盛り」、すなわち1/1,000です。

ADCの分解能は、最大信号入力レンジをいくつの部分に分割できるかを示す指標です。振幅分解能は、ADCの離散出力レベルの数により制限されます。各区分はバイナリコードで表します。つまり、レベルの数は以下のように計算できます。

^{式9:ADCの離散出力レベルの計算}

たとえば、3ビットのオシロスコープには2の3乗、つまり8つのレベルがあります。また、16ビットのオシロスコープには2の16乗、つまり65,536のレベルがあります。検出可能な最小電圧変化、つまりコード幅は以下のように計算できます。

^{式9: ADCの離散出力レベルの計算}

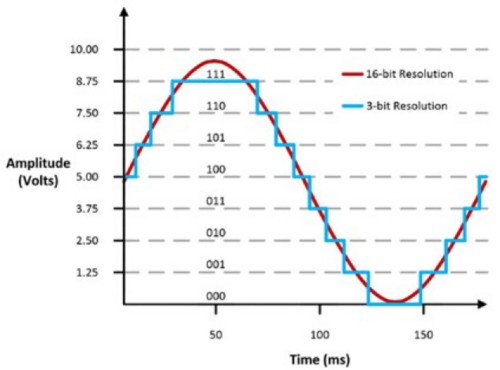
コード幅は最下位ビット (LSB) とも呼ばれます。デバイス入力範囲が0～10 Vの場合、3ビットのオシロスコープのコード幅は10/8 = 1.25 Vになり、16ビットのオシロスコープのコード幅は10/65,536 = 305 μVになります。どの分解能のオシロスコープで信号を集録するかによって、入力信号の表示のされ方に大きな違いが生じる可能性があります。

^{図9:16ビットと3ビットの分解能で表現できる波形の違い}

必要な分解能は用途によって異なります。分解能が高いほど、オシロスコープの価格も高くなります。高分解能のオシロスコープは必ずしも確度が高いということではありません。ただし、計測器で実現可能な確度は分解能によって制限されます。分解能は測定の精度を制限します。つまり、分解能が高いほど (ビット数が高いほど)、測定はより精密になります。

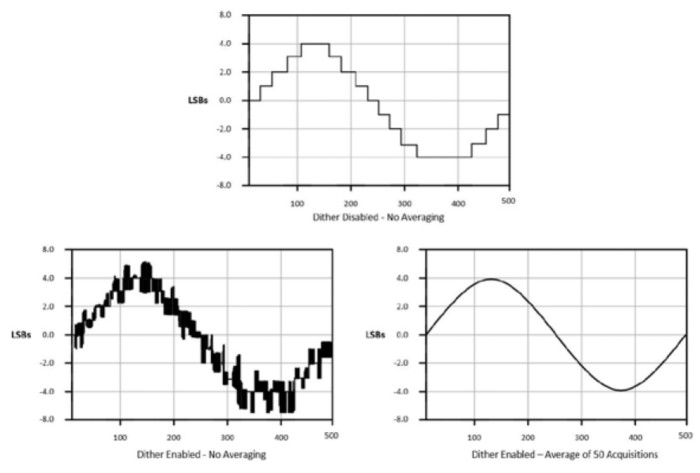
一部のオシロスコープではディザリングという方法を使用して、測定された信号を平滑化し、より高い分解能の信号として表示します。ここでディザリングとは、入力信号に意図的にノイズを加える作業を指します。これにより、振幅分解能のわずかな差分が平滑化されます。ランダムノイズを加える際は、隣接するレベル間を信号がバウンスするように加えることが重要です。当然ながら、これだけでは信号のノイズが大きくなるだけです。しかし、信号を集録した後、このノイズをデジタル平均化すると信号は平滑化されます。

^{図10:ディザリングで信号を平滑化できる}

• 帯域幅はオシロスコープで正確に測定可能な周波数の範囲を表します。帯域幅は、正弦波入力信号が本来の振幅の70.7%に減衰する周波数と定義され、-3 dBポイントとしても知られています。
• 帯域幅はコーナー周波数間の差です。
• 振幅誤差は、帯域幅と入力信号の周波数の比率を表すパーセンテージで、システム内のノイズの特定に役立ちます。
• 振幅誤差を最小限に抑えながら信号をキャプチャするには、オシロスコープの帯域幅を測定信号の対象となる最高周波数成分の3～5倍にすることを推奨します。
• 入力信号の立ち上がり時間は、最大信号振幅の10%から90%に信号が遷移するまでの時間です。
• 立ち上がり時間の誤差を最小限に抑えながら信号をキャプチャするには、オシロスコープの立ち上がり時間を測定信号の立ち上がり時間の1/3～1/5にすることを推奨します。
• サンプリングレートとは、ADCでアナログ入力波形がデジタルデータに変換される周波数のことです。
• サンプリングレートは、信号内の対象となる最高周波数の最低2倍以上である必要がありますが、ほとんどの場合は約5倍以上が必要です。
• エイリアシングは、サンプリングデータに不正確な周波数成分が現れる現象です。
• 分解能のビット数は、オシロスコープで信号の表現に使用可能な垂直レベルの数です。
• 計測器の分解能が高いほど、精度が高くなります。

• すべての計測器の基礎コンテンツをダウンロード