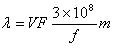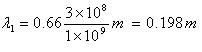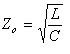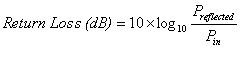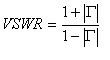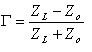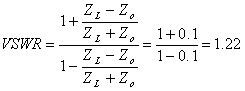Chapitre 1 : Comprendre les principales spécifications des commutateurs RF
Aperçu
Ce document constitue la première partie du Guide de sélection d’un commutateur RF. Ce guide en 5 parties rassemble des informations pertinentes qui vous permettront d’acquérir les connaissances nécessaires à la conception de votre réseau de commutation RF. Cette section décrit les spécifications de base des commutateurs RF, telles que la perte d’insertion, le ROS (rapport d’ondes stationnaires), l’impédance caractéristique et le temps de montée.
Pour en savoir plus sur l’offre de commutateurs RF de NI, consultez la page principale des commutateurs RF de NI
Contenu
- Introduction à la commutation RF
- Impédance caractéristique
- Perte d’insertion
- Rapport d’ondes stationnaires (ROS)
- Bande passante
- Topologie
- Isolation et diaphonie
- Temps de montée
- Conclusion
- Liens associés
Introduction à la commutation RF
Avec l’augmentation récente de la disponibilité des produits de commutation RF pour le développement de systèmes de test, il est de plus en plus difficile de choisir le bon produit pour votre application. La plupart des fournisseurs RF décrivent leurs produits de commutation RF en utilisant deux spécifications principales : la topologie et la bande passante (comme le multiplexeur NI PXI-2594 2.5 GHz 4x1). Bien que ces spécifications soient en effet importantes et vitales pendant la phase d’évaluation, elles ne fournissent pas suffisamment d’informations à l’acheteur pour qu’il puisse faire un choix éclairé. L’objectif de ce tutoriel est de vous présenter les sept spécifications importantes suivantes qui doivent être prises en compte lors de la conception de votre réseau de commutation RF :
- Impédance caractéristique
- Bande passante
- Topologie
- Perte d’insertion
- Perte de retour (RL) et rapport d’ondes stationnaires (ROS)
- Isolation et diaphonie
- Temps de montée
Avant d’aborder l’impédance caractéristique et les autres spécifications des commutateurs RF, il est important de comprendre la différence entre la propagation des signaux dans les circuits à courant continu et les systèmes RF. Dans les circuits à courant continu ou dans les circuits où le signal se propage à basse fréquence, la tension du signal en différents points d’un câble sur le trajet du signal varie très peu. Ce n’est pas le cas des signaux RF ou haute fréquence, dont la longueur d’onde est considérablement réduite par rapport à la longueur du câble, ce qui permet à plusieurs cycles du signal de se propager dans le câble en même temps.
Prenons l’exemple de deux ondes (signaux) de fréquences différentes qui se propagent à travers un câble coaxial de 1 m. La fréquence du premier signal est de 1 MHz et celle du second signal est de 1 GHz. Pour calculer leurs longueurs d’onde, nous utiliserons la formule suivante :
Dans la formule ci-dessus, « l » représente la longueur d’onde du signal, « f » sa fréquence et « VF » le facteur de vitesse du câble. Supposons que le câble coaxial utilisé pour acheminer les deux signaux soit de type RG8, dont le facteur de vélocité est connu pour être de 0,66.
Puis, pour
Signal 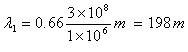
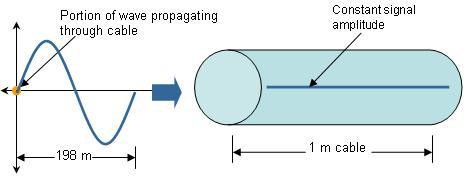
Figure 1. Une onde sinusoïdale de 1 MHz se propageant dans un câble coaxial de 1 m
Dans le cas du signal 1, la longueur du câble coaxial est considérablement réduite par rapport à la longueur d’onde du signal qui s'y propage. Par conséquent, comme le montre la figure 1, la variation du potentiel du signal à différents points du câble est négligeable.
Pour le signal 2 où f = 1 GHz :
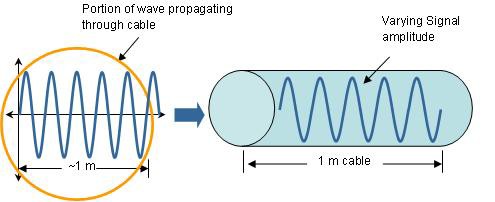
Figure 2. Une onde sinusoïdale de 1 GHz se propageant dans un câble coaxial de 1 m
Dans le cas du signal 2, la longueur du câble coaxial est beaucoup plus grande (presque 5 fois plus) que la longueur d’onde du signal qui s'y propage. Par conséquent, à tout moment, plusieurs cycles du signal circuleront simultanément dans le câble. En raison de leurs petites longueurs d’onde, les signaux haute fréquence traversent les câbles sous forme d’ondes. Ces signaux subissent donc des réflexions et des pertes de puissance lorsqu’ils se déplacent entre des milieux différents (théorie des ondes). Dans le cas des circuits électriques, cette variation de milieu se produit lorsque le signal (l’onde) traverse des composants du système qui ont des impédances caractéristiques variables. Par conséquent, pour minimiser les réflexions et les pertes de puissance, les systèmes RF doivent être construits en utilisant des composants appropriés avec des impédances adaptées. En règle générale, la dégradation du signal due à la perte de puissance et aux réflexions qui se produisent dans la ligne de transmission devient significative dès lors que la longueur du câble dépasse 0,01 de la longueur d’onde du signal qu’il sert à acheminer.
Impédance caractéristique
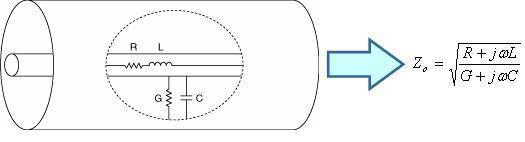
L’impédance caractéristique est un paramètre de la ligne de transmission qui est déterminé par la structure physique de la ligne. Il permet également de déterminer la manière dont les signaux de propagation sont transmis ou réfléchis dans la ligne. L’impédance des composantes RF n’est pas une résistance en courant continu et, dans le cas d’une ligne de transmission, elle peut être calculée à l’aide de la formule suivante :
Figure 3. Impédance caractéristique d’une ligne de transmission
Dans la formule ci-dessus :
Z0 = impédance caractéristique
L = inductance par longueur unitaire de la ligne de transmission RF causée par les champs magnétiques qui se forment autour des fils lorsque le courant les traverse.
C = capacité de la ligne de transmission RF par longueur unitaire Il s’agit aussi de la capacité qui existe entre deux conducteurs
R = résistance au courant continu de la ligne de transmission RF par longueur unitaire
G = la conductivité électrique par longueur
ω = fréquence (radians/s)
Comme un câble idéal ne présente ni résistance ni fuite diélectrique, son impédance caractéristique peut être calculée en utilisant la formule ci-dessus :
Comme tous les composants d’un système RF doivent être adaptés en termes d’impédance pour minimiser les pertes de signal et les réflexions, les fabricants de composants conçoivent spécifiquement leurs équipements pour qu’ils aient une impédance caractéristique de 50 ou 75 Ω. Les systèmes RF 50 Ω constituent la majeure partie du marché RF et incluent la plupart des systèmes de communication. Les systèmes RF 75 Ω sont moins nombreux et sont principalement répandus dans les systèmes vidéo RF. Il est essentiel que les ingénieurs s’assurent que les éléments tels que les câbles et les connecteurs, ainsi que les autres instruments qui peuvent se trouver dans le système de test, sont tous adaptés en matière d’impédance.
Perte d’insertion
Une perte de puissance significative du signal se produit si la longueur de la ligne de transmission dans laquelle il doit se propager est supérieure à 0,01 de sa propre longueur d’onde. La spécification de « perte d’insertion » d’un module de commutation est une mesure de cette perte de puissance et de l’atténuation du signal. La perte d'insertion d'un module de commutation à une fréquence particulière peut être utilisée pour calculer la perte de puissance ou l’atténuation de tension causée par le commutateur sur un signal à cette fréquence.
Formule pour calculer la perte de puissance :
Formule pour calculer l’atténuation de la tension :
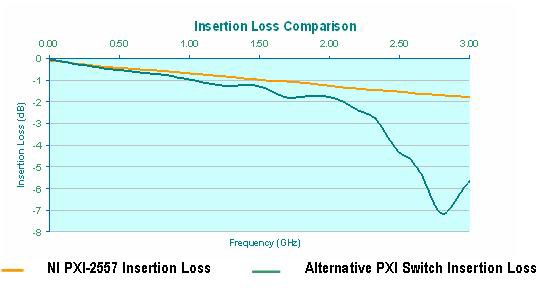
Pour comprendre le concept de perte d’insertion, pensez à un commutateur ou à un relais comme un filtre passe-bas. Dans le monde réel, chaque commutateur présente une capacité, une inductance, une résistance et une conductance parasites. Ces composants parasites se combinent pour atténuer et dégrader le signal utilisé par le commutateur. La perte de puissance et l’atténuation de la tension causées par ces composants varient en fonction de la fréquence du signal d’entrée et peuvent être quantifiées par les spécifications de perte d’insertion du module de commutation à cette fréquence. Il est donc essentiel de s’assurer que la perte d’insertion d’un commutateur est acceptable pour la largeur de bande requise par l’application. Pour comprendre pourquoi cela est important, prenons comme exemple la comparaison de l’adéquation de deux commutateurs pour une application RF particulière. Les exigences de l’application comprennent l’acheminement de huit signaux vidéo de 3 GHz vers un canal d’un analyseur de réseau vectoriel avec une atténuation inférieure à 30 % (la perte d’insertion doit être inférieure à 3 dB à 3 GHz). Le premier commutateur considéré est le multiplexeur NI PXI-2557 75 Ω 2.5 GHz 8x1, alors que le second est un multiplexeur 75 Ω 8x1 3 GHz d’un autre fournisseur PXI. Après un premier examen des spécifications de haut niveau des deux modules, il apparaît que le second serait plus approprié (il a une meilleure spécification de largeur de bande). Cependant, un examen plus approfondi des deux produits révèle que cette hypothèse ne se vérifie pas. Le graphique suivant présente les données d’insertion de 160 MHz à 3 GHz recueillies sur les deux modules de commutation.
Figure 4. Comparaison des pertes d’insertion pour les modules de commutation des fournisseurs A et B
Comme vous pouvez le voir, à 3 GHz, la perte d’insertion du module 2.5 GHz est d’environ 1,78 dB, alors que celle du commutateur 3 GHz est plus proche de 5,64 dB. À partir de ces valeurs, nous pouvons calculer la tension subséquente et la perte de puissance causée par les deux modules :
| NI PXI-2557 | Autre fournisseur PXI | |
| Atténuation de tension en % à 3 GHz | 18,3 | 47,8 |
| Perte de puissance en % à 3 GHz | 33,3 | 72,7 |
Tableau 1. Comparaisons des pourcentages de pertes de tension et de puissance
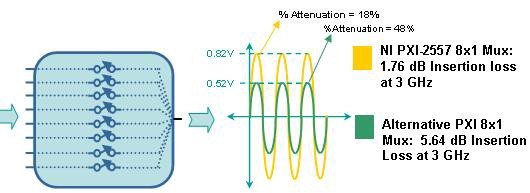
Les valeurs du tableau ci-dessus indiquent qu’une onde sinusoïdale de 3 GHz et 1 Vpp, lorsqu’elle traverse le multiplexeur NI PXI-2557 2.5 GHz 75 Ω, est atténué à 0,817 Vpp. Le même signal, lorsqu’il traverse par le multiplexeur 75 Ω de 3 GHz de l’autre fournisseur PXI, est atténué à 0,522 Vpp. On constate donc que même si la spécification de la largeur de bande du module de commutation de l’autre fournisseur PXI est plus élevée que celle du module NI, la dégradation nette du signal causée par ce dernier est nettement plus importante que celle causée par le NI PXI-2557. De plus, on peut affirmer que dans le cas de l’application à 3 GHz susmentionnée, le module de commutation NI de 2.5 GHz est mieux adapté que son homologue de 3 GHz.
Figure 5. Comparaison de l’atténuation causée par une onde sinusoïdale de 1 Vpp
Rapport d’ondes stationnaires (ROS)
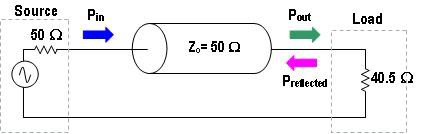
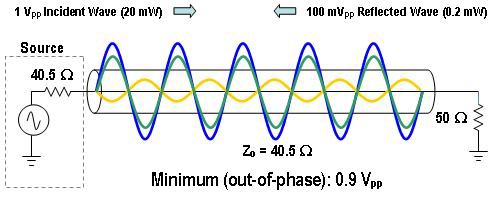
Le ROS est le rapport entre les ondes réfléchies et les ondes transmises. Comme mentionné précédemment, à des fréquences plus élevées, les signaux prennent la forme d’ondes lorsqu’ils traversent une ligne de transmission ou un câble. C’est pourquoi, tout comme dans le cas des ondes sonores et lumineuses, des réflexions se produisent lorsque le signal traverse différents supports (comme des composants dont l’impédance n’est pas adaptée). Dans un module de commutation, cette inadéquation peut se situer entre l’impédance caractéristique du connecteur, les pistes du circuit imprimé et le relais lui-même. Comme le ROS est une mesure de la puissance de l’onde réfléchie, il peut également être utilisé pour mesurer la perte de puissance dans la ligne de transmission. L’onde réfléchie, lorsqu’elle est additionnée au signal d’entrée, augmente ou diminue son amplitude nette, selon que la réflexion est en phase ou déphasée par rapport au signal d’entrée. Le rapport entre les tensions maximales (lorsque l’onde réfléchie est en phase) et minimales (lorsque l’onde réfléchie est déphasée) dans la configuration de « l’onde stationnaire » est connu sous le nom de ROS. Pour comprendre comment calculer le ROS et la parte de retour dans un système RF, considérons la ligne de transmission RF de la figure 6.
Figure 6. Comparaison de l’atténuation causée par une onde sinusoïdale de 1 Vpp
Dans le circuit de la figure 6, l’impédance de la charge (40,5 Ω) n’est pas égale à celle de la source et de la ligne de transmission (50 Ω). C’est pourquoi une partie du signal se propageant dans la ligne de transmission est réfléchie par la charge. Nous pouvons mesurer cette réflexion en utilisant la formule suivante :
Comme vous pouvez le voir, la perte de retour est une mesure de la puissance du signal réfléchi. Il s’agit également d’un sous-ensemble de la perte d’insertion. Plus la perte de retour (ou les réflexions) est élevée dans un système RF, plus sa perte d’insertion est élevée.
Le ROS est une autre façon de mesurer les réflexions du signal. Il peut être calculé comme suit :
Dans la formule ci-dessus, G est le coefficient de réflexion et peut être calculé à l’aide de la formule suivante :
Pour le circuit de la figure 6, nous calculons que le ROS est égal à :
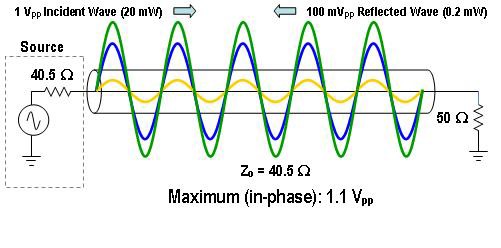
Pour visualiser ce qui se passe dans cet exemple, imaginons que le signal provenant du système RF soit une onde sinusoïdale de 1 Vpp. Comme le coefficient de réflexion du système est de 0,1, nous pouvons déterminer que l’amplitude de la réflexion est de 0,1 x 1 = 0,1 V ou 100 mV. La figure 7 montre les amplitudes maximale et minimale du signal résultant lorsque l’onde réfléchie est en phase et déphasée de 180 degrés par rapport au signal d’entrée, respectivement.
Figure 7. Tensions maximales et minimales dans l’onde stationnaire
Comme indiqué précédemment, le ROS est le rapport entre la tension maximale et la tension minimale dans le modèle d’onde stationnaire. En utilisant cette définition, nous pouvons calculer le ROS à partir de la figure 7 :
Bande passante
Comme mentionné précédemment, la bande passante d’un module de commutation est l’une de ses principales caractéristiques. Cependant, la bande passante ne nous fournit qu’une estimation approximative des performances d’un produit donné, car le processus d’établissement d’une spécification de largeur de bande passante pour un commutateur RF varie d’un fournisseur à l’autre. La largeur de bande d’un commutateur indique simplement le signal de fréquence maximale qui, selon le fournisseur, peut être acheminé à travers le commutateur avec une perte acceptable. Mais ce qui est acceptable pour un fournisseur ne l’est pas forcément pour un autre. Ainsi, un commutateur de 3 GHz du fournisseur A peut, par exemple, offrir des performances complètement différentes de celles d’un commutateur de 3 GHz du fournisseur B.
Reprenons l’exemple de deux modules fabriqués par des fournisseurs différents, dont la topologie et l’impédance caractéristique sont similaires, mais dont les spécifications en matière de largeur de bande sont différentes. Le premier module, le NI PXI-2557, est un multiplexeur 8x1 à 2.5 GHz avec une impédance caractéristique de 75 Ω ; le commutateur du fournisseur PXI alternatif est un multiplexeur 8x1 à 3 GHz avec une impédance caractéristique de 75 Ω. Bien que le deuxième module semble mieux adapté au routage des signaux entre 2 et 3 GHz, les données relatives à la perte d’insertion recueillies et présentées dans la figure 3 indiquent le contraire. C’est pourquoi la spécification de la bande passante du module NI est beaucoup plus conservatrice que celle de son homologue.
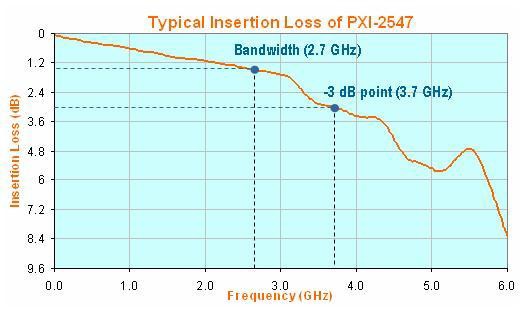
La bande passante d’un produit est aussi considérée, par beaucoup, comme sa largeur de bande à -3 dB. Ce point de vue est exact pour les instruments tels que les numériseurs où la spécification de la largeur de bande du périphérique est en fait le point -3 dB de la face-avant analogique de l’instrument. Cependant, pour un commutateur RF, la relation entre la bande passante et -3 dB n’est pas toujours vraie. Alors que certains fournisseurs spécifient effectivement la largeur de bande de -3 dB, d’autres ne le font pas. Le graphique de la figure 8, qui montre la perte d’insertion du NI PXI-2547 à sa largeur de bande (2.7 GHz) en conjonction avec son point à -3 dB (3.7 GHz), en est un exemple.
Figure 8. Perte d’insertion du multiplexeur NI PXI-2547 2.7 GHz 50 Ω 8x1
Topologie
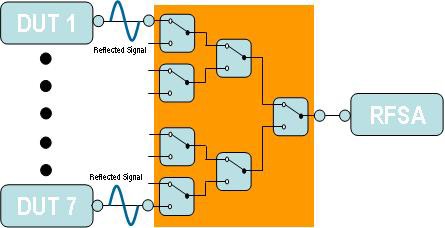
La topologie est l’une des caractéristiques les plus importantes à prendre en compte lors du choix d’un commutateur RF. Choisir un commutateur avec une mauvaise topologie peut avoir un impact considérable sur la perte d’insertion et le ROS. Les deux principaux types de topologies disponibles pour les RF sont les multiplexeurs et les relais SPDT (unipolaire bidirectionnel). Un multiplexeur est un système de commutation qui achemine séquentiellement plusieurs entrées vers une sortie ou vice versa. Un relais SPDT est une version réduite d’un multiplexeur. Un seul relais SPDT peut acheminer deux entrées vers une seule sortie ou vice versa. Les multiplexeurs RF sont souvent composés de plusieurs relais SPDT.
Différentes applications nécessitent différentes combinaisons de topologies de commutateurs RF. Par exemple, pour effectuer un test stimulus-réponse sur un matériel sous test (DUT) à 4 canaux, vous pouvez utiliser un module avec deux banques de multiplexage 4x1 individuelles. En revanche, pour un test qui effectue une analyse à partir des sorties de 8 DUT individuels, un module doté d’une seule banque 8x1 conviendrait mieux. En raison de la disponibilité de plusieurs commutateurs RF sur le marché, il est important de comprendre les utilisations optimales de ces différentes topologies afin de choisir la meilleure option pour votre application.
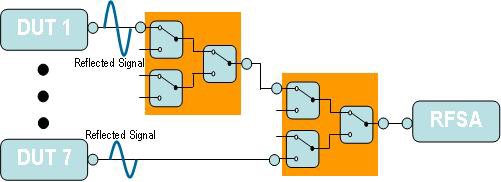
En abordant deux approches différentes de construction d’un multiplexeur 7x1, l’exemple des figures 9 et 10 montrera pourquoi l’une d’entre elles convient mieux que l’autre. La première approche met en cascade deux multiplexeurs 4x1 pour construire un seul multiplexeur 7x1. L’inconvénient de cette configuration est qu’elle requiert qu’un signal provenant d’un DUT passe par deux modules de commutation (quatre relais SPDT au total) avant d’atteindre l’analyseur de réseau vectoriel (VNA). Par conséquent, la perte d’insertion nette qui se produit sur le chemin du signal correspond désormais à la somme des spécifications de perte d’insertion individuelles de chaque relais et de chaque câble du système.
Figure 9. Deux multiplexeurs 4x1 en cascade
La seconde approche utilise un multiplexeur 8x1 inhérent (comme le multiplexeur NI PXI-2547 50 Ω 2.7 GHz 8x1) pour acheminer sept DUT vers le VNA. Cette configuration améliorera la perte d’insertion du système non seulement parce qu’elle réduit le nombre total de relais SPDT dans le chemin du signal (trois relais SPDT au lieu de quatre), mais aussi parce qu’elle élimine le câblage supplémentaire dans le système, comme les câbles qui existent entre les modules dans le système précédent. La qualité du signal qui atteint le VNA dans le second système est ainsi susceptible d’être bien meilleure que celle du premier.
Figure 10. Une topologie de multiplexeur 8x1 utilise moins de relais pour acheminer un signal que deux multiplexeurs 4x1.
Pour de plus amples informations sur le choix d’un commutateur disposant de la topologie la mieux adaptée à votre application, lisez le chapitre 2 du Guide de sélection d’un commutateur RF.
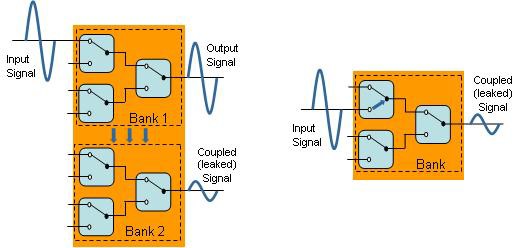
Isolation et diaphonie
On appelle isolation l’ampleur d’un signal qui est couplé à un circuit ouvert. La diaphonie est définie comme l’ampleur d’un signal couplé entre des circuits (tels que des bancs de multiplexage séparés sur un module RF).
Figure 11. Diaphonie vs isolation.
Temps de montée
Si un signal est purement sinusoïdal, les performances en matière de largeur de bande et de perte d’insertion d’un module de commutation suffisent à déterminer si le produit est adapté à l’application. Cependant, pour les signaux qui présentent plusieurs composantes de fréquence, comme les ondes carrées, cela peut ne pas être aussi simple, car le maintien de l’intégrité de ces signaux dépend de l’impact du commutateur sur le temps de montée du signal. Comme une onde carrée est composée d’un certain nombre d’ondes sinusoïdales dont la fréquence varie, pour obtenir une mesure précise, la bande passante du commutateur doit être suffisamment élevée pour provoquer une atténuation minimale sur tous les signaux sinusoïdaux individuels. En règle générale, pour une onde carrée, une fois que la 5e ou la 7eharmonique est atteinte, la variation du temps de montée est minime. Par conséquent, en général, une onde carrée peut être acheminée par un commutateur si le point -3 dB du commutateur (fréquence à laquelle la perte d’insertion est égale à 3 dB) correspond à 7X la fréquence fondamentale de l’onde carrée. Certains fournisseurs spécifient le temps de montée du commutateur. Dans ce cas, vérifiez que le temps de montée du module de commutation est inférieur au temps de montée de l’harmonique la plus élevée qui doit être acheminée avec une distorsion minimale.
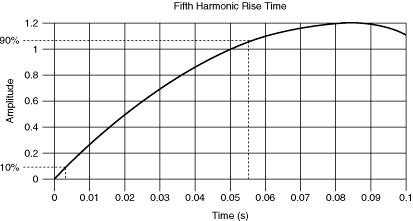
La figure ci-dessous montre la mesure du temps de montée pour la 5eharmonique d’une onde carrée. Supposons qu’il s’agisse de l’harmonique la plus élevée de l’onde carrée qui doit être acheminée par le commutateur. Pour déterminer si un commutateur particulier peut acheminer le signal avec succès, nous devons comparer le temps de montée du commutateur avec le temps de montée de l’harmonique. Parfois, cette spécification n’est pas disponible pour un module de commutation. Dans ce cas, nous pouvons calculer le point à -3 dB de cette harmonique et le comparer au point à -3 dB du commutateur. Le point -3 dB peut être calculé à partir du temps de montée en utilisant la formule :
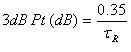
Figure 12. Cinquième harmonique d’une onde carrée
Pour le signal illustré dans la figure ci-dessus, nous calculons que la fréquence à laquelle -3 dB est atteint est de 6,36 Hz (le temps de montée est de 0,055 s). Par conséquent, un commutateur dont la perte d’insertion est inférieure à 3 dB à 6,36 Hz ou plus sera suffisant pour acheminer l’onde carrée.
Conclusion
La spécification de la tension d’un instrument ou d’un commutateur est une limitation physique de ce périphérique. De même, la fréquence d’échantillonnage d’un numériseur et la précision d’un multimètre numérique décrivent bien la capacité maximale de l’instrument. Un numériseur à 200 MS/s ne peut pas atteindre une fréquence d’échantillonnage en temps réel supérieure à 200 MS/s. Cependant, un commutateur RF à 2 GHz peut acheminer des signaux supérieurs à 2 GHz, mais avec une perte de puissance plus importante. C’est pourquoi, afin de sélectionner le commutateur RF le meilleur ainsi que le plus rentable pour votre application, il est nécessaire d’examiner attentivement la fiche technique du produit pour déterminer si sa perte d’insertion, son ROS, son isolation et d’autres spécifications répondent aux exigences de votre système. Certains fournisseurs proposent des diagrammes indiquant ces spécifications pour toute une gamme de fréquences, tandis que d’autres ne fournissent des spécifications que pour une fréquence particulière. Dans de ce cas, il est important de contacter le fournisseur et de demander des spécifications plus complètes afin de déterminer si le produit est adapté à votre application.