Guide des mesures de fréquence - Comment la fréquence est-elle mesurée ?

La fréquence est le taux de récurrence d'un événement cyclique ou périodique. En physique, vous pouvez observer une périodicité dans les rotations, les oscillations et les ondes. Pour un signal analogique ou numérique, vous pouvez inverser la période du signal pour obtenir la fréquence. Plus la période est petite, plus la fréquence est élevée, et vice versa. Ce principe est illustré dans la figure 1 ; la forme d’onde tout en haut présente la fréquence la plus basse, et celle tout en bas, la fréquence la plus élevée.

^{Figure 1 : Récepteur électronique CA}

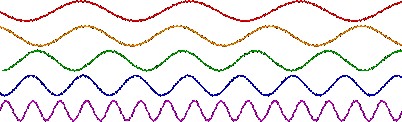
La fréquence est généralement représentée par la vitesse angulaire ω en radians/seconde, ou par la fréquence ƒ en secondes-1, ce qui correspond à l’unité hertz (Hz). Vous pouvez également utiliser les battements par minute (BPM) et les tours par minute (RPM pour revolutions per minute) pour représenter la fréquence. La vitesse angulaire ω (rad/sec) et la fréquence ƒ (Hz) sont liées par la formule suivante : ω =2πƒ. La fréquence est en général associée à une phase φ, qui décrit un décalage de l'onde par rapport à un point de référence spécifié au temps initial t0, et qui est généralement exprimée en degrés ou radians. Si on prend l'exemple d'une onde sinusoïdale, la forme d'onde s’exprime en fonction du temps de la manière suivante , A étant l’amplitude, ω la vitesse angulaire et φ la phase.

Les signaux analogiques périodiques dans les applications réelles sont complexes et peuvent rarement être représentés par une simple sinusoïde. L'analyse de Fourier est utilisée pour décomposer toute forme d'onde complexe en une somme de fonctions plus simples, que ce soit sous forme de sinus et cosinus, ou sous forme d’exponentielles complexes. Les composantes fréquentielles qui constituent un tel signal représentent souvent les propriétés intéressantes, et cette analyse est connue sous le nom d'analyse de domaine fréquentiel ou spectrale. Ce type d'analyse est nécessaire principalement pour les applications dans le domaine du son et des vibrations et ne sera pas abordé dans ce white paper.

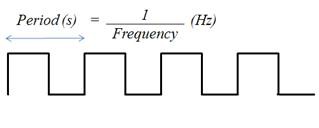
Obtenir la fréquence d'un signal numérique, en revanche, est assez simple. Pour un signal numérique simple, tel que celui représenté sur la figure 2, la période correspond au temps écoulé entre les fronts montants, ou même entre les fronts descendants.

^{Figure 2. Signal numérique}

Si le temps entre les fronts montants ou descendants varie légèrement, vous pouvez en calculer la moyenne sur un grand nombre d’échantillons pour déterminer la fréquence.

Pour une acquisition de fréquence numérique, le processus est assez simple. Pour les signaux basse fréquence, il suffit d'utiliser un compteur, ou base de temps. Le front montant du signal en entrée déclenche le nombre de tops de la base de temps à compter. La fréquence de la base de temps étant connue, vous pouvez facilement calculer la fréquence du signal en entrée (voir figure 3).

^{Figure 3. Signal numérique par rapport à la base de temps interne (un seul compteur pour les basses fréquences)}

Lorsque la fréquence du signal numérique est très élevée ou variable, il est préférable d’opter pour l’une des méthodes utilisant deux compteurs décrites ci-dessous. Notez que la même limitation matérielle s'applique aux deux méthodes à deux compteurs. C’est-à-dire que la fréquence que vous mesurez ne peut pas dépasser la fréquence d’entrée maximale prise en charge par le compteur, même si elle peut dépasser celle de la base de temps interne. 

Méthode de mesure à deux compteurs pour les hautes fréquences

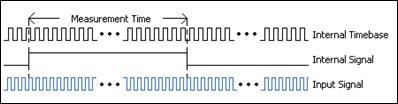
Pour un signal haute fréquence, vous avez besoin de deux compteurs. Un double compteur (deux compteurs) génère un train d’impulsions avec une période spécifiée par l’utilisateur, le « temps de mesure » (Measurement Time, voir Figure 4), beaucoup plus grande que celle du signal que vous mesurez, mais suffisamment petite pour empêcher la remise à zéro du compteur.

^{Figure 4. Fréquence du signal numérique mesurée avec deux compteurs (haute fréquence)}

Le temps de mesure de ce signal interne (Internal Signal) doit être un multiple de la base de temps interne (Internal Timebase), ou, en d’autres termes, divisé. Le nombre de tops du signal en entrée (Input Signal) est ensuite compté pendant la période de temps connue fournie par le signal interne. En divisant le nombre de tops par le temps de mesure connu, on obtient la fréquence du signal en entrée.

Méthode de mesure de gamme étendue à deux compteurs

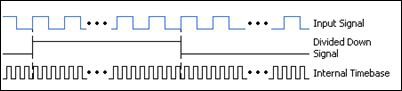
Pour les signaux présentant des variations de fréquence, cette méthode à double compteur offre une exactitude accrue sur toute la gamme. Dans ce cas, le signal en entrée (Input Signal) est divisé par une valeur connue, ou diviseur. Le nombre de tops de la base de temps interne (Internal Timebase) est compté sur un niveau logique haut du signal divisé (Divided Down Signal, voir figure 5). Cela donne le temps du niveau logique haut, qui est le produit du nombre de tops comptés par la période de la base de temps interne. Il suffit alors de multiplier ce temps par deux pour obtenir la période du signal divisé (temps haut et bas), qui est un multiple de la période du signal en entrée. En prenant l’inverse de la période du signal en entrée, on obtient alors sa fréquence.

^{Figure 5. Fréquence du signal numérique mesurée avec deux compteurs (gamme étendue)}

Cette méthode revient à faire la moyenne des valeurs sur une gamme plus longue pour tenir compte de la variation du signal, mais vous pouvez également utiliser cette méthode pour mesurer des signaux avec des fréquences plus élevées que la base de temps.

Connexion d’un signal numérique à un instrument pour compter la fréquence

De nombreux appareils dotés d’un cadencement matériel peuvent convenir pour les mesures de compteur. Prenons comme exemple un système NI CompactDAQ (voir Figure 6). La base de temps du matériel pour le NI CompactDAQ est située sur le fond de panier du châssis et n’est pas spécifique aux modules NI de la Série C. 

^{Figure 6. Châssis NI cDAQ-9178 et module d’E/S numériques NI 9401}

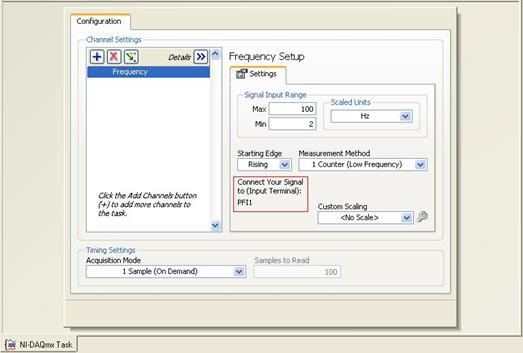
Le module NI 9401 comporte un connecteur Sub-D qui permet de connecter les huit voies numériques. Chaque voie dispose d’une broche d’E/S numériques à laquelle vous pouvez connecter un périphérique d’entrée ou de sortie numérique. L’accès aux quatre compteurs du châssis CompactDAQ est disponible à partir de tous les emplacements du châssis. Après avoir configuré l’acquisition de fréquence comme tâche de compteur dans Measurement & Automation Explorer (MAX), le terminal d’entrée PFI auquel vous devriez connecter votre signal est indiqué (voir Figure 7).

^{Figure 7. Capture d’écran de la configuration dans Measurement & Automation Explorer (MAX)}

Visualisation des mesures : NI LabVIEW

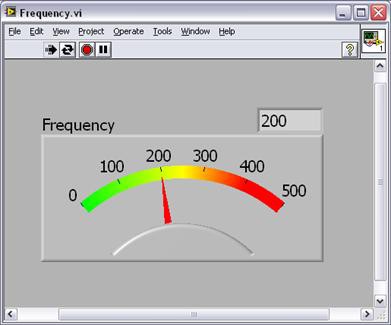
Une fois le système configuré, vous pouvez visualiser les données à l’aide de l’environnement de programmation graphique LabVIEW (voir Figure 8).

^{Figure 8. Mesure de fréquence telle qu’affichée dans LabVIEW}

• Exemple de système de mesure de fréquence
• Tutoriel d’initiation à CompactDAQ et FlexLogger
• Tutoriel d’initiation au matériel CompactDAQ et à LabVIEW
• Découvrir et tester gratuitement le logiciel LabVIEW

• Effectuer des mesures de fréquence précises
• Options de formation utiles : Acquisition de données et conditionnement de signal
• Choisir une méthode de mesure de fréquence par compteur pour un périphérique NI DAQ
• Comment puis-je déterminer l’erreur de fréquence et l’exactitude de la génération ou de la mesure de fréquence ?
• Synchronisation des entrées analogiques et des mesures de fréquence par compteur
• Mesure de fréquence maximale pour les périphériques d’acquisition de données NI