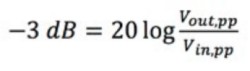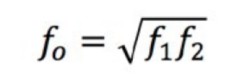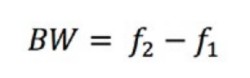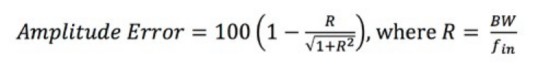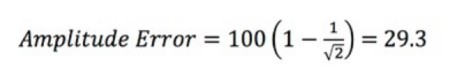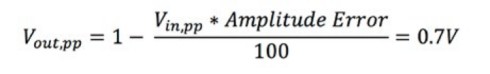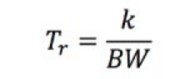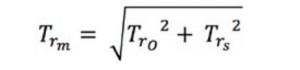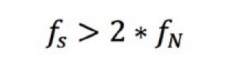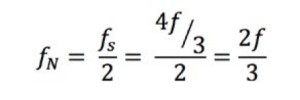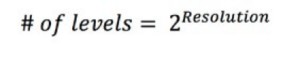Acquisition d’un signal analogique : bande passante, théorème d’échantillonnage de Nyquist et repliement

Les scientifiques et les ingénieurs utilisent souvent un numériseur pour capturer des données analogiques dans le monde réel et les convertir en signaux numériques pour analyse. Un numériseur fait référence à tout dispositif utilisé pour convertir des signaux analogiques en signaux numériques. Le téléphone cellulaire est l’un des numériseurs les plus courants. Il convertit une voix, un signal analogique, en un signal numérique à envoyer à un autre téléphone. Cependant, dans les applications de test et de mesure, un numériseur est le plus souvent un oscilloscope ou un multimètre numérique (DMM). Cet article se concentre sur les oscilloscopes, mais la plupart des sujets sont également applicables aux autres numériseurs.

Quel que soit son type, le numériseur est essentiel pour que le système puisse reconstruire avec précision une waveform. Pour vous assurer de choisir l’oscilloscope approprié pour votre application, tenez compte de la bande passante, de la fréquence d’échantillonnage et de la résolution de l’oscilloscope. 

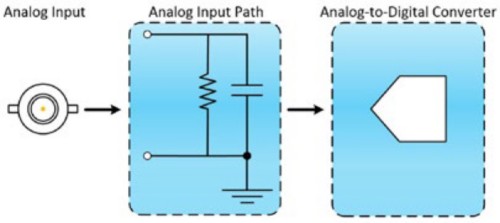
Le frontal d’un oscilloscope se compose de deux éléments : un chemin d’entrée analogique et un convertisseur analogique-numérique (C A/N). Le chemin d’entrée analogique atténue, amplifie, filtre et/ou couple le signal pour l’optimiser en vue de sa numérisation par le C A/N. Le C A/N échantillonne la waveform conditionnée et convertit le signal d’entrée analogique en valeurs numériques qui représentent la waveform d’entrée analogique. La réponse en fréquence du chemin d’entrée provoque une perte inhérente d’informations d’amplitude et de phase.

La bande passante décrit la capacité du frontal analogique à acheminer un signal du monde extérieur vers le C A/N avec une perte d’amplitude minimale, de la pointe de la sonde ou du dispositif de test à l’entrée du C A/N. Autrement dit, la bande passante décrit la gamme de fréquences qu’un oscilloscope peut mesurer avec précision.

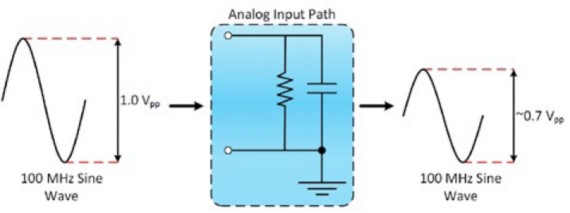
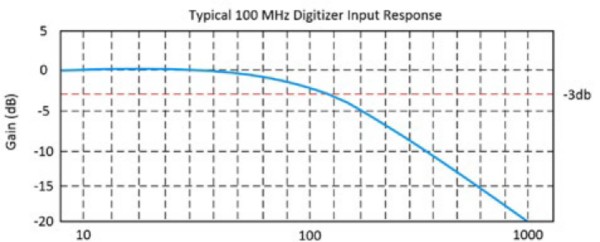
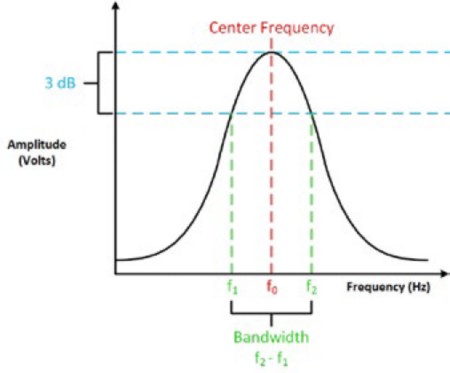
Elle est définie par la fréquence à laquelle un signal d’entrée sinusoïdal est atténué à 70,7 % de son amplitude d’origine, également connue sous le nom de point -3 dB. Les Figures 2 et 3 illustrent la réponse typique en entrée d’un oscilloscope 100 MHz.

^{Figure 1 : La bande passante décrit la gamme de fréquences dans laquelle le signal d’entrée peut traverser le frontal de l’oscilloscope, qui se compose de deux éléments : un chemin d’entrée analogique et un C A/N.}

^{Figure 2 : On parle de bande passante lorsque le signal d’entrée est atténué à 70,7 % de son amplitude d’origine.}  

^{Figure 3 : Ce graphique indique qu’à 100 MHz, le signal d’entrée atteint le point -3 dB.}  

La bande passante est mesurée entre les points de fréquence inférieure et supérieure où l’amplitude du signal tombe à -3 dB en dessous de la fréquence de la bande passante. Cela semble compliqué, mais lorsque vous décomposez le processus, il est en fait relativement simple. 

Tout d’abord, il est nécessaire de calculer votre valeur -3 dB.

^{Équation 1 : Calcul du point -3 dB.}

V_in,pp correspond à la tension pic à pic du signal d’entrée et V_out,pp fait référence à la tension pic à pic du signal de sortie. Par exemple, si vous appliquez la formule illustrée dans l’Équation 1, V_{out, pp} serait approximativement égal à 0,7 V.

Étant donné que le signal d’entrée est sinusoïdal, il existe deux fréquences auxquelles le signal de sortie atteint cette tension. Il s’agit des fréquences de coupure f₁ et f₂. Ces deux fréquences portent de nombreux noms différents tels que fréquence de coude, fréquence de bruit, fréquence de coude du bruit, fréquence de coupure demi-puissance, fréquence de 3 dB et fréquence de pause. Cependant, tous ces termes font référence aux mêmes valeurs. La fréquence centrale, f₀, du signal est la moyenne géométrique de f₁ et f₂.

^{Équation 2 : Calcul de la fréquence centrale.}

Vous pouvez calculer la bande passante (BP) en soustrayant les deux fréquences de coupure. 

^{Équation 3 : Calcul de la de bande passante} 

^{Figure 4 : La bande passante, la fréquence de coupure, la fréquence centrale et le point -3 dB sont tous associés.}

Calcul de l’erreur d’amplitude

Une autre équation qui se révèle souvent utile est l’erreur d’amplitude.  

^{Équation 4 : Calcul de l’erreur d’amplitude.}

L’erreur d’amplitude est exprimée en pourcentage. R correspond au rapport entre la bande passante de l’oscilloscope et la fréquence du signal en entrée (f_in).

Dans l’exemple ci-dessus, nous avons un oscilloscope 100 MHz avec un signal d’entrée sinusoïdal de 100 MHz à 1 V, BP = 100 MHz et (f_in) = 100 MHz. Cela signifie que R = 1. Ensuite, il suffit de résoudre l’équation :

L’erreur d’amplitude est de 29,3 %. Vous pouvez alors déterminer la tension de sortie pour le signal de 1 V :

Il est recommandé que la bande passante de votre oscilloscope soit de trois à cinq fois la composante de fréquence la plus élevée d’intérêt dans le signal mesuré pour capturer le signal avec une erreur d’amplitude minimale. Par exemple, pour le signal sinusoïdal de 1 V à 100 MHz, vous devriez utiliser un oscilloscope avec une bande passante de 300 à 500 MHz. Les erreurs d’amplitude d’un signal de 100 MHz à ces bandes passantes sont les suivantes :

Calcul du temps de montée

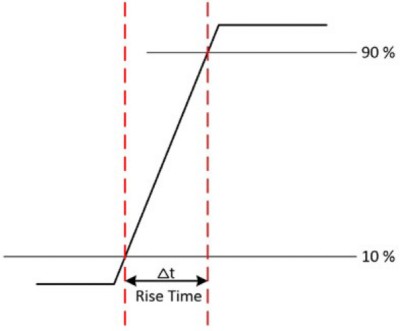
Un oscilloscope doit disposer de la bande passante appropriée pour mesurer avec précision le signal, mais il doit également avoir un temps de montée suffisant pour capturer avec exactitude les détails des transitions rapides. Cela est particulièrement applicable si vous mesurez des signaux numériques tels que des impulsions et des étapes. Le temps de montée d’un signal d’entrée correspond au temps nécessaire pour qu’un signal passe de 10 % à 90 % de l’amplitude maximale du signal. Certains oscilloscopes peuvent utiliser de 20 à 80 %, assurez-vous donc de consulter votre manuel d’utilisation.

^{Figure 5 : Le temps de montée d’un signal d’entrée correspond au temps nécessaire pour qu’un signal passe de 10 % à 90 % de l’amplitude maximale du signal.}

Le temps de montée (Tr) peut être calculé comme suit :

^{Équation 5 : Calcul du temps de montée.}

La constante k dépend de l’oscilloscope. Pour la plupart des oscilloscopes avec une bande passante inférieure à 1 GHz, k = 0,35, tandis que pour les oscilloscopes avec une bande passante supérieure à 1 GHz, la valeur k est généralement comprise entre 0,4 et 0,45.

Le temps de montée théorique, T_r-m, peut être calculé à partir du temps de montée de l’oscilloscope T_r-o et du temps de montée réel du signal d’entrée, T_r-s, en utilisant la formule suivante.

^{Équation 6 : Calcul du temps de montée théorique mesuré.}

Il est recommandé que le temps de montée de l’oscilloscope soit d’un tiers à un cinquième du temps de montée du signal mesuré pour capturer le signal avec une erreur de temps de montée minimale.

La fréquence d’échantillonnage n’est pas directement liée aux spécifications de bande passante. Il s’agit de la fréquence à laquelle le C A/N convertit le signal d’entrée analogique en données numériques. L’oscilloscope échantillonne le signal après avoir appliqué une atténuation, un gain ou un filtrage au chemin d’entrée analogique et convertit la waveform résultante en représentation numérique. Il effectue ce processus en instantanés, comme les images d’un film. Plus les échantillons de l’oscilloscope sont rapides, plus la résolution et les détails visibles dans la waveform sont élevés. 

Théorème d’échantillonnage de Nyquist

Le théorème d’échantillonnage de Nyquist explique la relation entre la fréquence d’échantillonnage et la fréquence du signal mesuré. Il stipule que la fréquence d’échantillonnage f_s doit être supérieure au double de la composante de fréquence la plus élevée d’intérêt du signal mesuré. Cette fréquence est souvent appelée fréquence de Nyquist, f_N. 

^{Équation 7 : La fréquence d’échantillonnage doit être supérieure au double de la fréquence de Nyquist.} 

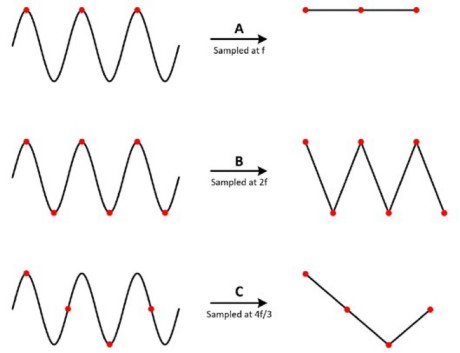
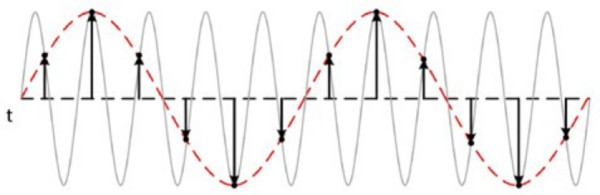
Pour comprendre pourquoi, jetez un œil à un signal sinusoïdal mesuré à différentes vitesses. Dans le cas A, le signal sinusoïdal de fréquence f est échantillonné à cette même fréquence. Ces échantillons sont marqués sur le signal d’origine à gauche et, lorsqu’ils sont construits à droite, le signal apparaît de manière erronée comme une tension continue constante. Dans le cas B, la fréquence d’échantillonnage correspond au double de la fréquence du signal. Elle apparaît maintenant comme un signal triangulaire. Dans ce cas, f est égal à la fréquence de Nyquist, qui est la composante de fréquence la plus élevée permise pour éviter le repliement pour une fréquence d’échantillonnage donnée. Dans le cas C, la fréquence d’échantillonnage est de 4f/3. La fréquence de Nyquist est alors la suivante :

Comme la valeur f est plus grande que la fréquence de Nyquist, cette fréquence d’échantillonnage reproduit un signal replié de fréquence et de forme incorrectes.

Ainsi, pour reconstruire avec précision la waveform, la fréquence d’échantillonnage fs doit être supérieure au double de la composante de fréquence la plus élevée d’intérêt du signal mesuré. En général, il est préférable d’échantillonner environ à une fréquence cinq fois plus élevée que la fréquence du signal.

^{Figure 6 : Une fréquence d’échantillonnage trop basse peut provoquer une reconstruction inexacte de la waveform.} 

Repliement

Vous devez échantillonner à une certaine fréquence pour éviter le repliement. Mais qu’est-ce que le repliement exactement ? Si un signal est échantillonné à une fréquence inférieure au double de la fréquence de Nyquist, de fausses composantes de fréquence inférieure apparaissent dans les données échantillonnées. Ce phénomène est appelé repliement. La figure suivante montre un signal sinusoïdal de 800 kHz échantillonné à 1 Méch./s. La ligne en pointillés indique le signal replié enregistré à cette fréquence d’échantillonnage. La fréquence de 800 kHz se replie dans la bande passante, apparaissant de manière erronée comme un signal sinusoïdal de 200 kHz.

^{Figure 7 : Un repliement se produit lorsqu’une fréquence d’échantillonnage est trop basse et reproduit une représentation de waveform inexacte.}

La fréquence de repliement f_a peut être calculée pour déterminer de quelle manière un signal d’entrée à une fréquence supérieure à la fréquence de Nyquist apparaît. Il s’agit de la valeur absolue du multiple entier le plus proche de la fréquence d’échantillonnage moins la fréquence du signal d’entrée. 

^{Équation 8 : Calcul de la fréquence de repliement.}

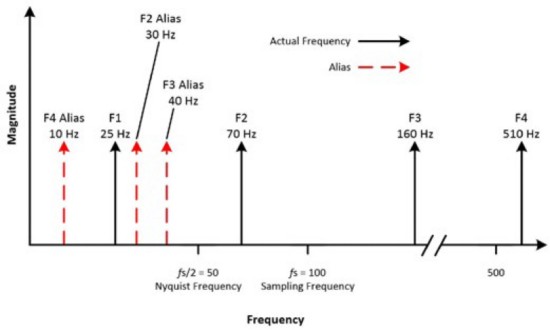
Par exemple, considérons un signal avec une fréquence d’échantillonnage de 100 Hz et le signal d’entrée contient les fréquences suivantes : 25 Hz, 70 Hz, 160 Hz et 510 Hz. Les fréquences inférieures à la fréquence de Nyquist de 50 Hz sont échantillonnées correctement ; celles supérieures à 50 Hz apparaissent avec un repliement. 

^{Figure 8 : Différentes valeurs de fréquence sont mesurées, dont certaines sont des fréquences de repliement et d’autres des fréquences réelles de la waveform.}

Les calculs des fréquences de repliement sont les suivants : 

En plus d’augmenter la fréquence d’échantillonnage, le repliement peut également être évité en utilisant un filtre anti-repliement. Il s’agit d’un filtre passe-bas qui atténue toutes les fréquences du signal d’entrée supérieures à la fréquence de Nyquist et qui doit être introduit avant le C A/N pour restreindre la bande passante du signal d’entrée afin de répondre aux critères d’échantillonnage. Les voies d’entrée analogique peuvent disposer de filtres analogiques et numériques implémentés dans le matériel afin de faciliter la prévention du repliement.

La résolution est un autre facteur à prendre en compte lors de la sélection d’un oscilloscope pour une application. Les bits de résolution font référence au nombre de niveaux verticaux uniques qu’un oscilloscope peut utiliser pour représenter un signal. Le concept de résolution peut être expliqué en effectuant une comparaison avec un étalon. Divisez un mètre-étalon en millimètres : quelle est la résolution ? Le plus petit repère sur l’étalon correspond à la résolution, soit 1 sur 1000.

La résolution d’un C A/N dépend du nombre de parties en lesquelles le signal maximal peut être divisé. La résolution d’amplitude est limitée par le nombre de niveaux de sortie discrets d’un C A/N. Un code binaire représente chaque division. À ce titre, le nombre de niveaux peut être calculé comme suit :

^{Équation 9 : Calcul des niveaux de sortie discrets d’un C A/N.}

Par exemple, un oscilloscope 3 bits dispose de 23 ou 8 niveaux. En revanche, un oscilloscope 16 bits dispose de 216 ou 65 536 niveaux. Le changement de tension (ou largeur de code) minimum détectable peut être calculé comme suit :

^{Équation 9 : Calcul des niveaux de sortie discrets d’un C A/N.}

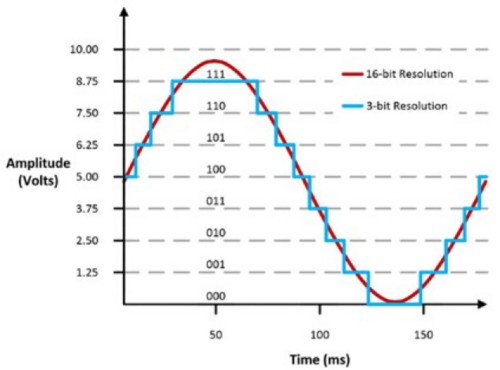
La largeur de code est aussi appelée bit de poids faible (LSB). Si la gamme d’entrée du dispositif est de 0 à 10 V, un oscilloscope 3 bits a une largeur de code de 10/8 = 1,25 V, tandis qu’un oscilloscope 16 bits a une largeur de code de 10/65 536 = 305 μV. Cela peut faire grandement différer la manière dont le signal est affiché.

^{Figure 9 : Différence d’une waveform entre 16 bits et 3 bits de résolution.}

La résolution dont vous avez besoin dépend de votre application. Plus la résolution est élevée, plus l’oscilloscope coûte cher. Gardez à l’esprit qu’un oscilloscope avec une haute résolution ne signifie pas nécessairement qu’il effectue des mesures haute exactitude. L’exactitude réalisable d’un instrument est toutefois limitée par la résolution. La résolution limite la précision d’une mesure. Plus la résolution (nombre de bits) est élevée, plus la mesure est précise.

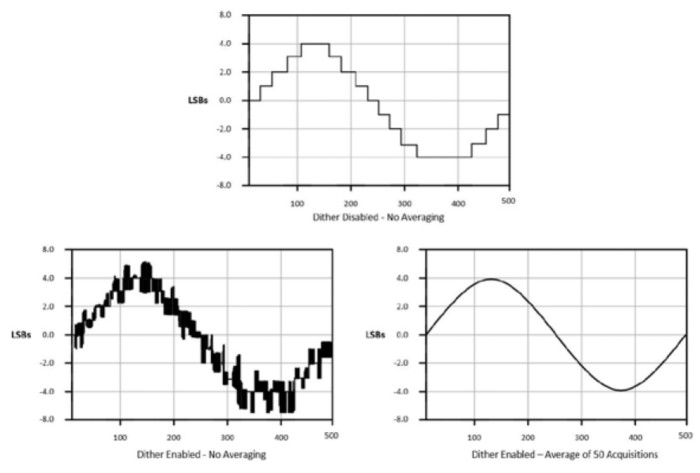
Certains oscilloscopes utilisent une méthode appelée « dithering » pour faciliter le lissage des signaux afin d’obtenir l’apparence d’une résolution plus élevée. Le dithering implique l’ajout délibéré de bruit au signal d’entrée. Les petites différences de résolution d’amplitude sont ainsi atténuées. La clé de cette méthode est d’ajouter du bruit aléatoire de manière à ce que le signal fasse des allers-retours entre les niveaux successifs. Bien sûr, davantage de bruit est présent sur le signal. Mais une fois le signal acquis, il se lisse en faisant la moyenne numérique de ce bruit.

^{Figure 10 : Le dithering peut permettre de lisser un signal.} 

• La bande passante décrit la gamme de fréquences qu’un oscilloscope peut mesurer avec précision. Elle est définie par la fréquence à laquelle un signal d’entrée sinusoïdal est atténué à 70,7 % de son amplitude d’origine, également connue sous le nom de point -3 dB.
• La bande passante correspond à la différence entre les fréquences de coupure.
• L’erreur d’amplitude est un pourcentage correspondant au rapport de la bande passante avec les fréquences du signal d’entrée qui aide à déterminer le bruit dans un système.
• Il est recommandé que la bande passante de votre oscilloscope soit de trois à cinq fois la composante de fréquence la plus élevée d’intérêt dans le signal mesuré pour capturer le signal avec une erreur d’amplitude minimale.
• Le temps de montée d’un signal d’entrée correspond au temps nécessaire pour qu’un signal passe de 10 % à 90 % de l’amplitude maximale du signal.
• Il est recommandé que le temps de montée de l’oscilloscope soit d’un tiers à un cinquième du temps de montée du signal mesuré pour capturer le signal avec une erreur de temps de montée minimale.
• La fréquence d’échantillonnage fait référence à la fréquence à laquelle le C A/N convertit le signal d’entrée analogique en données numériques.
• La fréquence d’échantillonnage devrait être au moins deux fois plus élevée que la fréquence d’intérêt du signal, mais la plupart du temps, elle devrait être environ cinq fois plus élevée.
• Le repliement se produit lorsque de fausses composantes de fréquence apparaissent dans les données échantillonnées.
• Les bits de résolution font référence au nombre de niveaux verticaux uniques qu’un oscilloscope peut utiliser pour représenter un signal.
• Plus la résolution d’un instrument est élevée, plus la précision est accrue.

• Télécharger tout le contenu sur les principes fondamentaux des instruments