Explicación sobre el controlador PID y la teoría

Un controlador PID es un instrumento que recibe datos de entrada de sensores, calcula la diferencia entre el valor real y el punto de ajuste deseado y ajusta las salidas para controlar variables como temperatura, tasa del flujo, velocidad, presión y voltaje. Lo hace a través de tres mecanismos: control proporcional, que reacciona al error de corriente; control integral, que aborda errores acumulados en el pasado; y control derivado, que predice errores futuros. El controlador PID suma esos tres componentes para calcular la salida. Esta arquitectura permite a los controladores PID mantener de manera eficiente el control del proceso y la estabilidad del sistema. Antes de comenzar a definir los parámetros de un controlador PID, analicemos qué es un sistema de ciclo cerrado y algunas de las terminologías asociadas con él.

Sistema de ciclo cerrado

En un sistema de control típico, la variable de proceso es el parámetro del sistema que debe controlarse, como la temperatura (°C), la presión (psi) o la tasa de flujo (litros/minuto). Se utiliza un sensor para medir la variable del proceso y proporcionar retroalimentación al sistema de control. El punto de referencia es el valor deseado o de comando para la variable del proceso, como 100 grados Celsius en el caso de un sistema de control de temperatura. En cualquier momento dado, la diferencia entre la variable del proceso y el punto de referencia es utilizada por el algoritmo del sistema de control (compensador) para determinar la salida deseada del para accionar el sistema (planta). Por ejemplo, si la variable del proceso de temperatura medida es 100 °C y el punto de referencia de temperatura deseado es 120 °C, entonces la salida del actuador especificada por el algoritmo de control podría ser para accionar un calentador. Provocar que un actuador se encienda un calentador hace que el sistema se caliente y da como resultado un aumento en la variable del proceso de temperatura. Esto se denomina sistema de control de ciclo cerrado, porque el proceso de lectura de sensores para proporcionar una retroalimentación constante y calcular la salida deseada del actuador se repite continuamente y a una tasa de ciclo fija, como se ilustra en la figura 1.

En muchos casos, la salida del actuador no es la única señal que tiene un efecto en el sistema. Por ejemplo, en una cámara de temperatura puede haber una fuente de aire frío que a veces entra en la cámara y altera la temperatura. Este término se conoce como perturbación. Por lo general, tratamos de diseñar el sistema de control para minimizar el efecto de las perturbaciones en la variable del proceso.

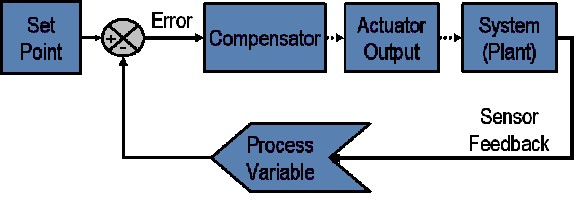
^{Figura 1: Diagrama de bloques de un sistema típico de ciclo cerrado.}

Definición de terminologías

El proceso del diseño de control comienza con la definición de los requisitos de rendimiento. Por lo general, el rendimiento del sistema de control se mide aplicando una función de paso como la variable de comando del punto de referencia y luego midiendo la respuesta de la variable del proceso. Comúnmente, la respuesta se cuantifica midiendo características de forma de onda definidas. El tiempo de incremento es la cantidad de tiempo que tarda el sistema en pasar del 10% al 90% del valor de estado estable o final. El porcentaje de sobreimpulso es la cantidad en que la variable del proceso excede el valor final, expresado como un porcentaje del valor final. El tiempo de estabilización es el tiempo requerido para que la variable del proceso se estabilice dentro de un cierto porcentaje (comúnmente 5%) del valor final. El error de estado estable es la diferencia final entre la variable del proceso y el punto de referencia. Tenga en cuenta que la definición exacta de estas cantidades variará en la industria y la academia.

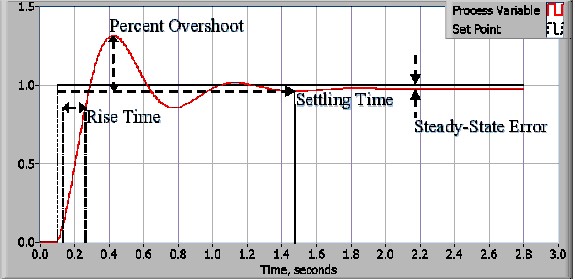
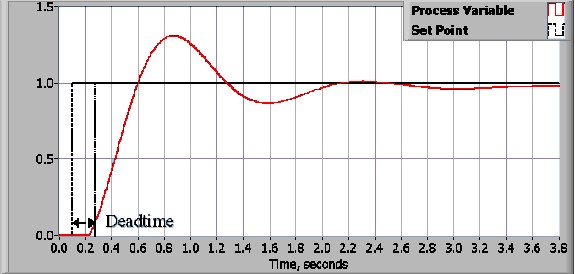
Una vez que se han especificado los requisitos de rendimiento, es hora de examinar el sistema y seleccionar un esquema de control apropiado. En la gran mayoría de las aplicaciones, un control PID proporcionará los resultados requeridos

Respuesta proporcional

El componente proporcional depende únicamente de la diferencia entre el punto de referencia y la variable del proceso. Esta diferencia se conoce como el término error. La ganancia proporcional (K_c) determina la relación entre la respuesta de salida y la señal de error. Por ejemplo, si el término de error tiene una magnitud de 10, una ganancia proporcional de 5 produciría una respuesta proporcional de 50. En general, aumentar la ganancia proporcional aumentará la velocidad de respuesta del sistema de control. Sin embargo, si la ganancia proporcional es demasiado grande, la variable del proceso comenzará a oscilar. Si K_c se aumenta aún más, las oscilaciones serán mayores y el sistema se volverá inestable e incluso puede oscilar fuera de control.

Respuesta integral

El componente integral suma el término de error en el transcurso del tiempo. El resultado es que incluso un término de error pequeño hará que el componente integral aumente lentamente. La respuesta integral aumentará continuamente con el tiempo a menos que el error sea cero, por lo que el efecto es llevar el error de estado estable a cero. El error de estado estable es la diferencia final entre la variable del proceso y el punto de referencia. Se produce un fenómeno llamado windup integral cuando la acción integral satura un controlador sin que el controlador conduzca la señal de error hacia cero.

Respuesta derivada

El componente derivado hace que la salida disminuya si la variable del proceso aumenta rápidamente. La respuesta derivada es proporcional a la tasa de cambio de la variable del proceso. Aumentar el parámetro de tiempo derivado (T_d) hará que el sistema de control reaccione con más fuerza a los cambios en el término de error y aumentará la velocidad de respuesta del sistema de control en general. Los sistemas de control más prácticos utilizan un tiempo derivado muy pequeño (T_d ), porque la respuesta derivada es muy sensible al ruido en la señal de la variable del proceso. Si la señal de retroalimentación del sensor es ruidosa o si la tasa del ciclo de control es demasiado lenta, la respuesta derivada puede hacer que el sistema de control sea inestable

El proceso de establecer las ganancias óptimas para P, I y D para obtener una respuesta ideal desde un sistema de control se denomina sintonización. Existen diferentes métodos de sintonización de los cuales se discutirán el método de "adivinar y comprobar" y el método de Ziegler Nichols.

Las ganancias de un controlador PID se pueden obtener con un método de prueba y error. Una vez que un ingeniero comprende la importancia de cada parámetro de ganancia, este método se vuelve relativamente fácil. En este método, los términos I y D se establecen en cero primero y la ganancia proporcional se aumenta hasta que la salida del ciclo oscila. A medida que se aumenta la ganancia proporcional, el sistema se vuelve más rápido, pero debe tener cuidado de no volverlo inestable. Una vez que se ha establecido P para obtener una respuesta rápida deseada, el término integral se aumenta para detener las oscilaciones. El término integral reduce el error de estado estable, pero aumenta el sobreimpulso. Siempre es necesaria cierta cantidad de sobreimpulso para que un sistema rápido pueda responder de inmediato a los cambios. El término integral se modifica para lograr un mínimo error de estado estable. Una vez que P e I se han configurado para obtener el sistema deseado de control rápido con un mínimo error de estado estable, el término derivado se aumenta hasta que el ciclo es aceptablemente rápido hasta su punto de referencia. Aumentar el término derivado disminuye el sobreimpulso y produce una mayor ganancia con estabilidad, pero provocaría que el sistema fuera muy sensible al ruido. Muchas veces, los ingenieros necesitan intercambiar una característica de un sistema de control por otra para cumplir mejor con sus requisitos.

El método Ziegler-Nichols es otro método popular para sintonizar un controlador PID. Es muy similar al método de prueba y error en el que I y D se establecen en cero y P se aumenta hasta que el ciclo comienza a oscilar. Una vez que comienza la oscilación, se anotan la ganancia crítica K_c y el período de oscilaciones P_c. P, I y D luego se ajustan según la columna tabular que se muestra a continuación.

La herramienta LabVIEW PID presenta una amplia variedad de VIs que ayudan enormemente en el diseño de un sistema de control basado en PID. La limitación del rango de salida de control, el integrador anti-windup y la salida del controlador sin impactos para los cambios de ganancia de PID son algunas de las características más destacadas del VI de PID. El PID Advanced VI incluye todas las características del PID VI junto con acción integral no lineal, control de dos grados de libertad y control elevado al cuadrado.

^{Figura 5: VIs de la paleta de controles PID de LabVIEW}

La paleta PID también cuenta con algunos VIs avanzados como el PID Autotuning VI y el PID Gain Schedule VI. El PID Autotuning VI ayuda a refinar los parámetros de PID de un sistema de control. Una vez que se ha hecho una suposición informada sobre los valores de P, I y D, el PID Autotuning VI ayuda a refinar los parámetros PID para obtener una mejor respuesta del sistema de control.

La fiabilidad del sistema de controles mejora enormemente al usar el módulo LabVIEW Real Time que se ejecuta en un dispositivo en tiempo real. NI proporciona dispositivos de adquisición de datos que brindan mayor precisión y mejor rendimiento que un sistema de control promedio

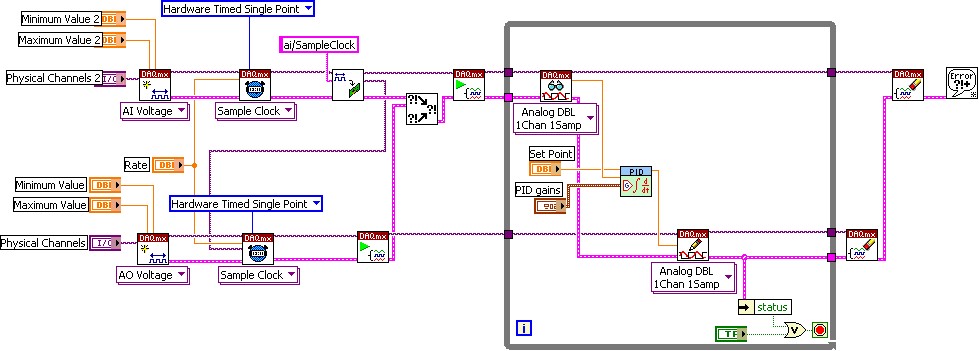
^{Figura 7: Un VI de LabVIEW típico muestra control PID con un dispositivo de adquisición de datos de NI insertable}

La perfecta integración de estos dispositivos de adquisición de datos con LabVIEW minimiza el tiempo de desarrollo involucrado y aumenta enormemente la productividad de cualquier ingeniero. La Figura 7 muestra un VI típico en LabVIEW que muestra el control PID utilizando la API del controlador NI-DAQmx, que se incluye con el hardware de adquisición de datos de NI.

El algoritmo de control PID es un algoritmo robusto y simple que se utiliza ampliamente en la industria. El algoritmo tiene suficiente flexibilidad para producir excelentes resultados en una amplia variedad de aplicaciones y ha sido una de las principales razones del uso continuo a lo largo de los años. NI LabVIEW y los dispositivos insertables de adquisición de datos de NI ofrecen mayor precisión y mejor rendimiento para hacer un excelente sistema de control PID.

1. Control PID clásico
por Graham C. Goodwin, Stefan F. Graebe, Mario E. Salgado
Diseño de sistemas de control, Prentice Hall PTR

2. Control PID de procesos continuos
por John W. Webb Ronald A. Reis
Controladores lógicos programables, cuarta edición, Prentice Hall PTR