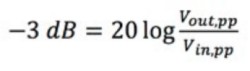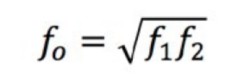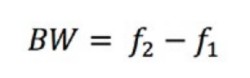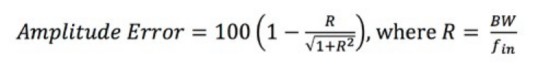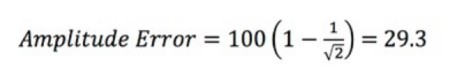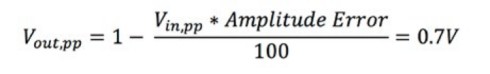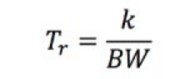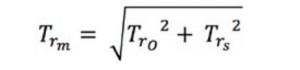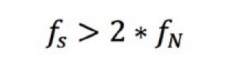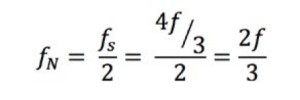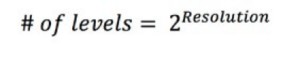Adquirir una señal analógica: ancho de banda, teorema de muestreo de Nyquist y aliasing

Los científicos e ingenieros a menudo usan un digitalizador para capturar datos analógicos en el mundo real y convertirlos en señales digitales para su análisis. Un digitalizador es cualquier dispositivo que se utiliza para convertir señales analógicas en señales digitales. Uno de los digitalizadores más comunes es un teléfono celular, que convierte una voz, una señal analógica, en una señal digital para enviar a otro teléfono. Sin embargo, en aplicaciones de pruebas y medidas, un digitalizador generalmente se refiere a un osciloscopio o un multímetro digital (DMM). Este artículo se centra en los osciloscopios, pero la mayoría de los temas también se aplican a otros digitalizadores.

Independientemente del tipo, el digitalizador es vital para que el sistema reconstruya con precisión una forma de onda. Para asegurarse de seleccionar el osciloscopio correcto para su aplicación, considere el ancho de banda, la velocidad de muestreo y la resolución del osciloscopio. 

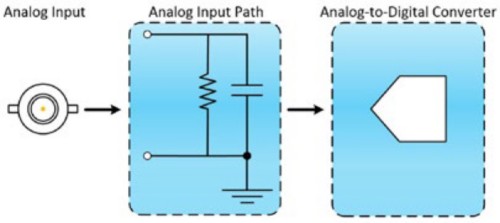
El frente de un osciloscopio consta de dos componentes: una ruta de entrada analógica y un convertidor analógico a digital (ADC). La ruta de entrada analógica atenúa, amplifica, filtra y/o acopla la señal para optimizarla en preparación para la digitalización por parte del ADC. El ADC muestrea la forma de onda acondicionada y convierte la señal de entrada analógica en valores digitales que representan la forma de onda de entrada analógica. La respuesta de frecuencia de la ruta de entrada provoca una pérdida inherente de información de amplitud y fase.

El ancho de banda describe la capacidad del frente analógico para obtener una señal del mundo exterior al ADC con una pérdida de amplitud mínima, desde la punta de la sonda o el dispositivo de prueba hasta la entrada del ADC. En otras palabras, el ancho de banda describe el rango de frecuencias que un osciloscopio puede medir con precisión.

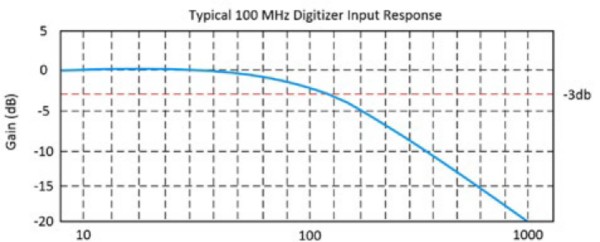
Se define por la frecuencia a la que una señal de entrada sinusoidal se atenúa al 70.7% de su amplitud original, que también se conoce como el punto -3 dB. Las Figuras 2 y 3 muestran la respuesta de entrada típica para un osciloscopio de 100 MHz.

^{Figura 1: El ancho de banda describe el rango de frecuencia en el que la señal de entrada puede pasar a través del frente del osciloscopio, que está formado por dos componentes: una ruta de entrada analógica y un ADC.}

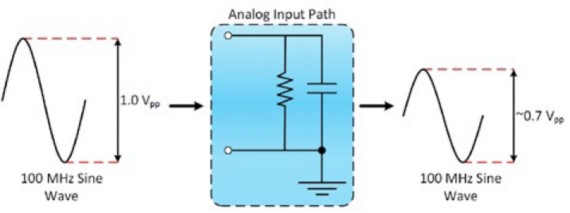
^{Figura 2: El ancho de banda es cuando la señal de entrada se atenúa al 70.7% de su amplitud original.}  

^{Figura 3: Esta gráfica indica que a 100 MHz, la señal de entrada llega al punto -3dB.}  

El ancho de banda se mide entre los puntos de frecuencia inferior y superior donde la amplitud de la señal cae a -3 dB por debajo de la frecuencia de pasobanda. Esto suena complicado, pero cuando lo desglosa, en realidad es relativamente fácil. 

Primero, debe calcular su valor de -3 dB.

^{Ecuación 1: Calcular el punto de -3 dB.}

V_{in, pp} es el voltaje pico a pico de la señal de entrada y V_{out, pp} es el voltaje pico a pico de la señal de salida. Por ejemplo, si aplica la fórmula que se muestra en la Ecuación 1, V_{out, pp} sería aproximadamente igual a 0.7 V.

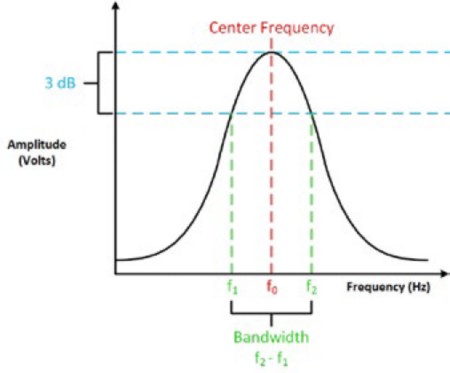
Debido a que la señal de entrada es una onda sinusoidal, hay dos frecuencias en las que la señal de salida alcanza este voltaje; estas se llaman frecuencias de esquina f₁ y f₂. Estas dos frecuencias tienen muchos nombres diferentes, como frecuencia de esquina, frecuencia de corte, frecuencia de cruce, frecuencia de media potencia, frecuencia 3 dB y frecuencia de corte. Sin embargo, todos estos términos se refieren a los mismos valores. La frecuencia central, f₀, de la señal es la media geométrica de f₁ y f₂.

^{Ecuación 2: Calcular la frecuencia central.}

Puede calcular el ancho de banda (BW) restando las dos frecuencias de esquina. 

^{Ecuación 3: Calcular el ancho de banda} 

^{Figura 4: El ancho de banda, la frecuencia de esquina, la frecuencia central y el punto de 3 dB están todos conectados.}

Calcular el error de amplitud

Otra ecuación que suele ser útil es para el error de amplitud.  

^{Ecuación 4: Calcular el error de amplitud.}

El error de amplitud se expresa como un porcentaje y R es la relación entre el ancho de banda del osciloscopio y la frecuencia de la señal de entrada (f_in).

Usando el ejemplo anterior, tiene un osciloscopio de 100 MHz con una señal de entrada de onda sinusoidal de 100 MHz a 1 V y BW = 100 MHz y (f_in) = 100 MHz. Esto significa que R = 1. Entonces solo tienes que resolver la ecuación:

El error de amplitud es del 29.3%. Luego puede determinar el voltaje de salida para la señal de 1 V:

Se recomienda que el ancho de banda de su osciloscopio sea de tres a cinco veces el componente de interés de frecuencia más alta en la señal medida para capturar la señal con un error de amplitud mínimo. Por ejemplo, para la onda sinusoidal de 1 V a 100 MHz, debe usar un osciloscopio con un ancho de banda de 300 MHz a 500 MHz. El error de amplitud de una señal de 100 MHz en estos anchos de banda son:

Calcular el tiempo de incremento

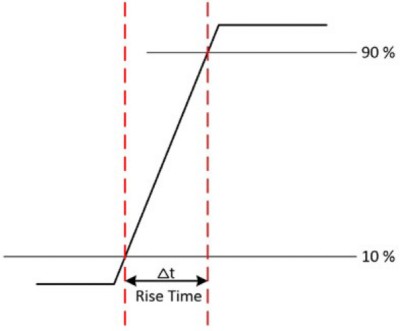
Un osciloscopio debe tener el ancho de banda adecuado para medir con precisión la señal, pero también debe tener suficiente tiempo de incremento para capturar con precisión los detalles de las transiciones rápidas. Esto es más aplicable si se miden señales digitales como pulsos y pasos. El tiempo de incremento de una señal de entrada es el tiempo que tarda una señal en pasar del 10% al 90% de la amplitud máxima de la señal. Algunos osciloscopios pueden usar del 20 al 80%, así que asegúrese de consultar su manual de usuario.

^{Figura 5: El tiempo de incremento de una señal de entrada es el tiempo que tarda una señal en pasar del 10% al 90% de la amplitud máxima de la señal.}

El tiempo de incremento (Tr) se puede calcular de la siguiente manera:

^{Ecuación 5: Calcular el tiempo de incremento.}

La constante k depende del osciloscopio. La mayoría de los osciloscopios con un ancho de banda inferior a 1 GHz suelen tener k = 0.35, mientras que los osciloscopios con un ancho de banda superior a 1 GHz suelen tener un valor de k entre 0.4 y 0.45.

El tiempo de incremento teórico, T_rm, se puede calcular a partir del tiempo de incremento del osciloscopio T_r-o y el tiempo de incremento real de la señal de entrada, T_r-s, utilizando la siguiente fórmula.

^{Ecuación 6: Cálculo del tiempo de incremento teórico medido.}

Se recomienda que el tiempo de incremento del osciloscopio sea de un tercio a un quinto del tiempo de incremento de la señal medida para capturar la señal con un error mínimo de tiempo de incremento.

La velocidad de muestreo, no está directamente relacionada con la especificación del ancho de banda. La velocidad de muestreo es la frecuencia a la que el ADC convierte la forma de onda de entrada analógica en datos digitales. El osciloscopio muestrea la señal después de que se haya aplicado cualquier atenuación, ganancia y/o filtrado a la ruta de entrada analógica y convierte la forma de onda resultante en una representación digital. Lo hace en imágenes instantáneas, similar a los marcos de una película. Cuanto más rápido muestree el osciloscopio, mayor será la resolución y el detalle que se puede ver en la forma de onda. 

Teorema de muestreo de Nyquist

El teorema de muestreo de Nyquist explica la relación entre la velocidad de muestreo y la frecuencia de la señal medida. Establece que la velocidad de muestreo f_s debe ser mayor que el doble del componente de interés de frecuencia más alta en la señal medida. Esta frecuencia a menudo se conoce como la frecuencia de Nyquist, f_N. 

^{Ecuación 7: La velocidad de muestreo debe ser mayor que el doble de la frecuencia de Nyquist.} 

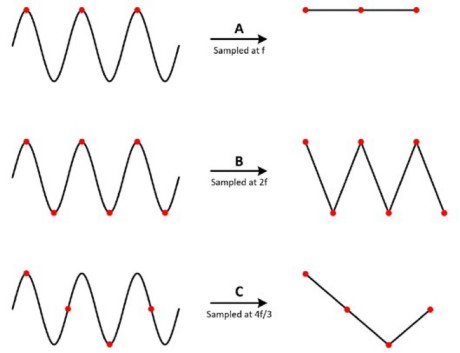
Para comprender por qué, observe una onda sinusoidal medida a diferentes velocidades. En el caso A, la onda sinusoidal de frecuencia f se muestrea a esa misma frecuencia. Esos muestreos están marcados en la señal original a la izquierda y, cuando se construyen a la derecha, la señal aparece incorrectamente como un voltaje DC constante. En el caso B, la velocidad de muestreo es el doble de la frecuencia de la señal. Ahora aparece como una forma de onda triangular. En este caso, f es igual a la frecuencia de Nyquist, que es el componente de frecuencia más alto permitido para evitar el aliasing para una frecuencia de muestreo determinada. En el caso C, la velocidad de muestreo es de 4f/3. La frecuencia de Nyquist en este caso es:

Debido a que f es mayor que la frecuencia de Nyquist, esta velocidad de muestreo reproduce una forma de onda alias de frecuencia y forma incorrectas.

Por lo tanto, para reconstruir con precisión la forma de onda, la velocidad de muestreo fs debe ser mayor que el doble del componente de interés de frecuencia más alta en la señal medida. Por lo general, debe muestrear alrededor de cinco veces más que la frecuencia de la señal.

^{Figura 6: Una velocidad de muestreo demasiado baja puede causar una reconstrucción inexacta de la forma de onda.} 

Aliasing

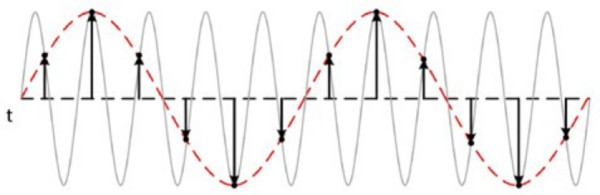
Si necesita muestrear a una cierta velocidad para evitar el aliasing, ¿qué es exactamente el aliasing? Si una señal se muestrea a una velocidad de muestreo menor que el doble de la frecuencia de Nyquist, aparecen componentes falsos de frecuencia más baja en los datos muestreados. Este fenómeno se conoce como aliasing. La siguiente figura muestra una onda sinusoidal de 800 kHz muestreada a 1 MS/s. La línea de puntos indica la señal con alias registrada a esa velocidad de muestreo. La frecuencia de 800 kHz vuelve a crear un alias en la banda de paso, apareciendo falsamente como una onda sinusoidal de 200 kHz.

^{Figura 7: El aliasing ocurre cuando una velocidad de muestreo es demasiado baja y reproduce una representación de forma de onda inexacta.} 

La frecuencia de alias f_a se puede calcular para determinar cómo aparece una señal de entrada a una frecuencia superior a la frecuencia de Nyquist. Es el valor absoluto del múltiplo entero más cercano de la frecuencia de muestreo menos la frecuencia de la señal de entrada. 

^{Ecuación 8: Calcular la frecuencia de alias.}

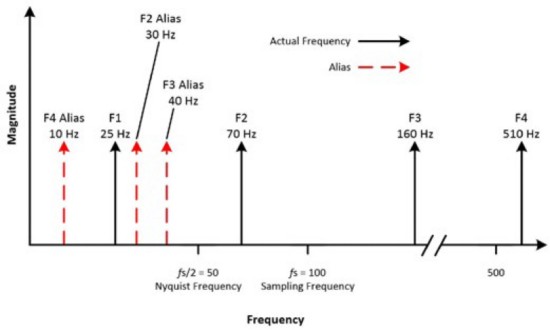
Por ejemplo, considere una señal con una frecuencia de muestreo de 100 Hz y la señal de entrada contiene las siguientes frecuencias: 25 Hz, 70 Hz, 160 Hz y 510 Hz. Las frecuencias por debajo de la frecuencia de Nyquist de 50 Hz se muestrean correctamente; aquellos por encima de 50 Hz aparecen como alias. 

^{Figura 8: Se miden diferentes valores de frecuencia, algunos de los cuales son frecuencias de alias y algunos de los cuales son frecuencias reales de la forma de onda.}

Estos son los cálculos para las frecuencias de alias: 

Además de aumentar la velocidad de muestreo, también se puede evitar el aliasing utilizando un filtro antialiasing. Este es un filtro de paso bajo que atenúa cualquier frecuencia en la señal de entrada que sea mayor que la frecuencia de Nyquist, y debe introducirse antes del ADC para restringir el ancho de banda de la señal de entrada para cumplir con los criterios de muestreo. Los canales de entrada analógica pueden tener filtros analógicos y digitales implementados en hardware para ayudar con la prevención de aliasing.

Otro factor a considerar al seleccionar un osciloscopio para una aplicación es la resolución. Los bits de resolución se refieren al número de niveles verticales únicos que un osciloscopio puede usar para representar una señal. Una forma de comprender el concepto de resolución es comparándolo con una vara de medir. Divida una medida de un metro en milímetros; ¿cuál es la resolución? La unidad más pequeña en la medida es la resolución, 1 en 1,000.

La resolución de un ADC es una función de en cuántas partes se puede dividir la señal máxima. La resolución de amplitud está limitada por el número de niveles de salida discreta que tiene un ADC. Un código binario representa cada división; como tal, el número de niveles se puede calcular de la siguiente manera:

^{Ecuación 9: Calcular los niveles de salida discreta de un ADC.}

Por ejemplo, un osciloscopio de 3 bits tiene 23 u ocho niveles. Un osciloscopio de 16 bits, por otro lado, tiene 216 o 65,536 niveles. El cambio de voltaje mínimo detectable o el ancho del código se puede calcular de la siguiente manera:

^{Ecuación 9: Calcular los niveles de salida discreta de un ADC.}

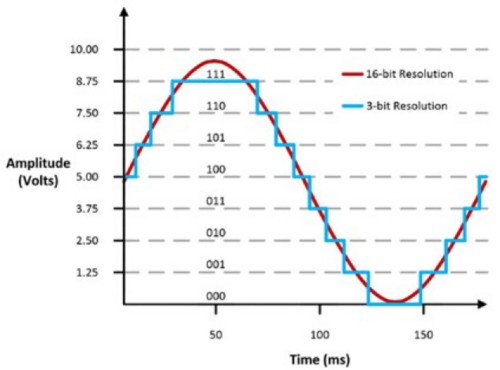
El ancho del código también se conoce como el bit menos significativo (LSB). Si el rango de entrada del dispositivo es de 0 a 10 V, entonces un osciloscopio de 3 bits tiene un ancho de código de 10/8 = 1.25 V, mientras que un osciloscopio de 16 bits tiene un ancho de código de 10/65,536 = 305 μV. Esto puede significar una gran diferencia en cómo se muestra la señal.

^{Figura 9: Diferencia de una forma de onda entre 16 bits y 3 bits de resolución.}

La resolución que necesita depende de su aplicación; cuanto mayor sea la resolución, más cuesta el osciloscopio. Tenga en cuenta que un osciloscopio con alta resolución no significa necesariamente que tenga una alta precisión. Sin embargo, la precisión alcanzable de un instrumento está limitada por la resolución. La resolución limita la precisión de una medida; cuanto mayor sea la resolución (número de bits), más precisa será la medida.

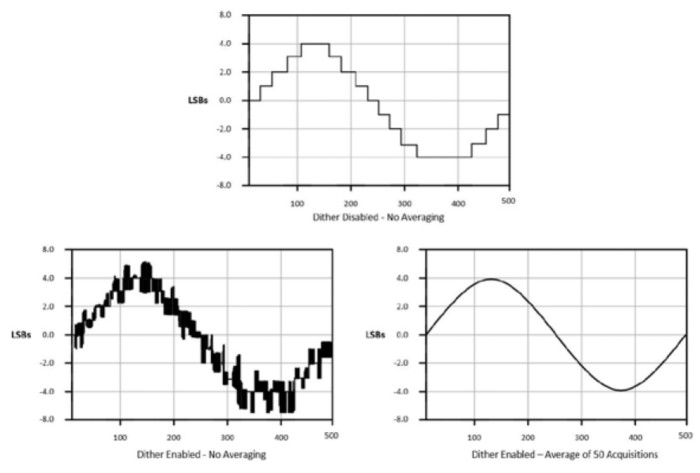
Algunos osciloscopios utilizan un método llamado dithering para ayudar a suavizar las señales para obtener la apariencia de una resolución más alta. El dithering implica la adición deliberada de ruido a la señal de entrada. Ayuda eliminando las pequeñas diferencias en la resolución de amplitud. La clave es agregar ruido aleatorio de una manera que haga que la señal rebote entre niveles sucesivos. Por supuesto, esto en sí mismo hace que la señal sea más ruidosa. Pero, la señal se suaviza al promediar este ruido digitalmente una vez que se adquiere la señal.

^{Figura 10: El dithering puede ayudar a suavizar una señal.} 

• El ancho de banda describe el rango de frecuencias que un osciloscopio puede medir con precisión. Se define por la frecuencia a la que una señal de entrada sinusoidal se atenúa al 70.7% de su amplitud original, que también se conoce como el punto -3 dB.
• El ancho de banda es la diferencia entre las frecuencias de esquina.
• El error de amplitud es un porcentaje que es la relación entre el ancho de banda y las frecuencias de la señal de entrada que ayuda a determinar el ruido en un sistema.
• Se recomienda que el ancho de banda de su osciloscopio sea de tres a cinco veces el componente de interés de frecuencia más alta en la señal medida para capturar la señal con un error de amplitud mínimo.
• El tiempo de incremento de una señal de entrada es el tiempo que tarda una señal en pasar del 10% al 90% de la amplitud máxima de la señal.
• Se recomienda que el tiempo de incremento del osciloscopio sea de un tercio a un quinto del tiempo de incremento de la señal medida para capturar la señal con un error mínimo de tiempo de incremento.
• La velocidad de muestreo es la frecuencia a la que el ADC convierte la forma de onda de entrada analógica en datos digitales.
• La velocidad de muestreo debe ser al menos el doble de la frecuencia más alta de interés en la señal, pero la mayor parte del tiempo debe ser alrededor de cinco veces mayor.
• Aliasing es cuando aparecen componentes de frecuencia falsa en los datos muestreados.
• Los bits de resolución se refieren al número de niveles verticales únicos que un osciloscopio puede usar para representar una señal.
• Cuanto mayor sea la resolución de un instrumento, mayor será la precisión.

• Descargar todo el contenido de fundamentos de instrumentos