Mastering Low-Power Validation for Enhanced Product Performance
Overview
In an increasingly connected world, electronic devices are becoming smarter, and the balance between battery performance and longevity has never been more important. A “low battery” alert creates a significant inconvenience regardless of the application. From wireless headphones at the gym to digital grocery lists on smartphones, consumers rely on battery-powered devices every day. What’s more, they expect these devices to stay powered on longer with a single charge. This means that engineers are consistently challenged with maximizing their electronics’ battery life.
One of the main requirements for extended battery life is being able to accurately measure the device’s total power consumption. The main challenge lies in the fact that the total load power is not limited to power-on and a steady-state operation but requires measurements in multiple operating states. Low-power conditions like sleep and transient states can generate incorrect data readings due to the low voltages that need to be measured, often in the nanovolt (nV) range. Additionally, some power events can last for short periods of time. This means that, in addition to needing highly accurate measurement instruments, having fast sampling rates is also a key consideration.
Contents
- Calculating Power Consumption on a Device with Multiple Power States
- Selecting the Right Measurement Device to Test Low-Power Circuits
- Evaluating the Instruments to Find the Right Fit for Low-Power Validation
- Next Steps
Calculating Power Consumption on a Device with Multiple Power States
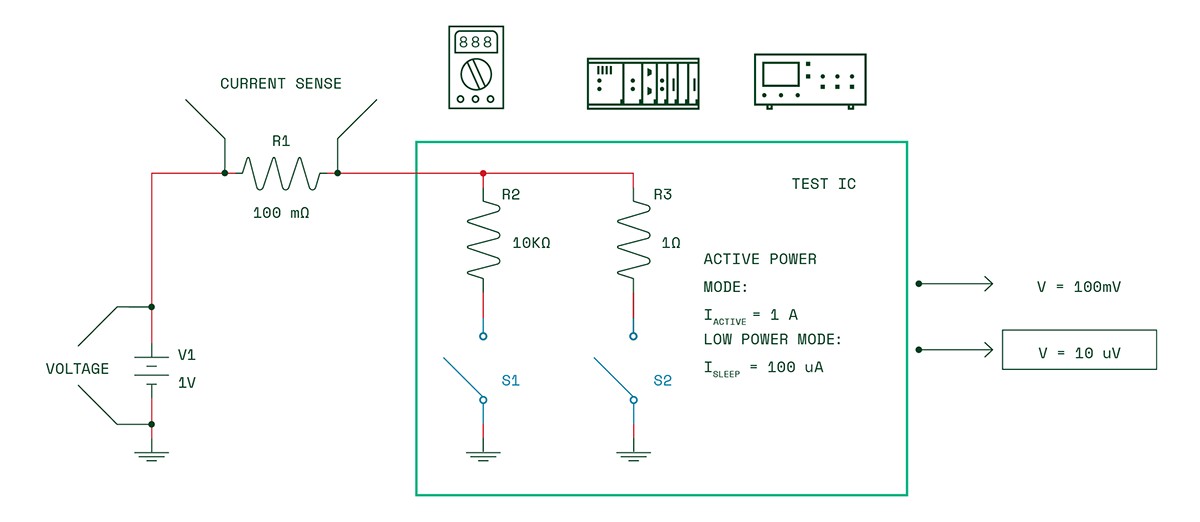
Accurately measuring power consumption of an electronic device requires an understanding of both the instrumentation options and the appropriate measurement setup. To illustrate, consider an example device in Figure 1. This diagram illustrates a simple circuit with two states: active- and low-power mode. V1 is the measured source voltage. This measurement is an important consideration for batteries because they lose power over time. Measuring power consumption requires a second voltage measurement across a current-sense resistor, which is labeled R1 in the diagram. R2 and R3 illustrate a representative load for the device under test, wherein R3 represents the active-power mode and R2 represents the low-power mode.
Figure 1: Circuit Example for Voltage Measurements in Active and Sleep States
V1 = Voltage source of 1 VDC
R1 = Current-sense resistor of 100 mΩ to measure voltage
R2 = Active-power-mode resistor of 10 kΩ
R3 = Low-power-mode resistor of 1 Ω
S1 and S2 = Switches to apply/simulate the load
The Importance of a Shunt Resistor
External shunt or current-sense resistors are an important aspect of power-consumption measurements. Measuring current consumption of a device with a voltage-measurement instrument such as a digital multimeter (DMM), data acquisition (DAQ) device, or oscilloscope requires careful attention to the sizing and tolerance of the shunt resistor. In this scenario, the shunt resistor is used to measure voltage drop and convert it to current. Sizing this resistor appropriately ensures accurate measurements.
In Figure 1, the R1 (100 mΩ, 0.1% tolerance) resistor represents the measured voltage drop that must be measured by an instrument. Here, we can use Ohm’s Law to calculate the expected voltage across the sense resistor. Note that the resistance should be low enough to decrease error yet large enough to allow for an accurate voltage-drop measurement. For our example, we chose 100 mΩ to enable an accurate current measurement while minimizing the power drawn by the measurement resistor.
Based on our model for both active- and low-power modes, we can estimate the expected voltage drop across our shunt resistor using the equations below. These calculations are the premises of voltage measurements and are fundamental when aiming to understand the accuracy of different instruments:
R2: lower-power-mode conditions
Expected current consumption = 1 VCD/10 kΩ = 100 uA
Expected voltage drop across shunt resistor = 100 uA x 100 mΩ = 10uV
Expected power consumption = 10 uV x 100 uA = 1 nW
R3: active-power-mode conditions
Expected current consumption = 1 VCD/1 Ω = 1 A
Expected voltage drop across shunt resistor = 1 A x 100 mΩ = 100 mV
Expected power consumption = 100 mV x 1 A = 100 mW
As we see above, the low-power-mode condition results in the smallest voltage drop across the shunt resistor. Because power consumption measurements are more challenging in this situation, we’ll focus on the accuracy calculations for the low-power condition.
Note that when a shunt resistor is used to measure power consumption, the total error of the measurement will consist of both the device error and the configuration error. For illustrative purposes, we’ll assume that any voltage drop across cabling and fixtures connected to the shunt resistor R1 and voltage source V1 are negligible. However, we can calculate the measurement error due to resistor tolerance using the equations below. Recall that in this example, the active-power-mode measurement is 100 mV and low-power mode is 10 uV:
R1 sense resistor value = 100mΩ, 0.1%
Sense resistor R1 error (V) = 10 uVv*0.1% = 10 nV
Sense resistor current error (A) = 10 nV/100 mΩ = 100 nA
Selecting the Right Measurement Device to Test Low-Power Circuits
When beginning to explore the world of voltage and current measurements, it’s vital to understand the relationship between voltage, current, and resistance. Because instrumentation generally measures either voltage or current, we’ll use Ohm’s Law to determine power consumption on the IC level, power rail, circuit, and/or system level. There are multiple options for performing low-power measurements, but each one comes with tradeoffs. The most common devices used to measure voltage are DMMs, oscilloscopes, and DAQ devices.
Using DMMs for Low-Power Readings
DMMs are one of the most common instruments for low-level voltage measurements. They typically utilize a wide range of features to correct voltage uncertainty. To determine the accuracy of this instrument, let’s consider a DMM (PXIe-4081) that features 7½-digit precision, ±1,000 V max input range, and an onboard 1.8 MS/s isolated digitizer. Table 1 was extracted from the specifications document. In this case, advanced DMM accuracy-enhancing features such as auto zero, ADC calibration, and offset nulling were disabled. It is important to understand that the overall accuracy for DMM can increase by 2 uV if DC offset nulling is enabled. Note that DC offset nulling is an advanced topic with a wide range of caveats and tradeoffs. For the purposes of this discussion, the measured voltage across the sense resistor will be 10 uV in the worst case, so we can ignore DC offset nulling for the time being.
Although we can use a DMM for both voltage- and current-measurement mode, we’ll evaluate a use case of a DMM in voltage-measurement mode with an external shunt resistor. This mode is often preferred for power-consumption measurements because it allows you to customize the value of the shunt resistor.
DC Voltage ± (ppm of reading + ppm of range)
| Range | Input Resistance1 | 24 HR2 TSELFCAL ± 1 °C | 90 Day TSELFCAL ± 5 °C | 2 Year TSELFCAL ± 5 °C | Tempco/°C | |
|---|---|---|---|---|---|---|
| Without Self-Cal | With Self-Cal | |||||
| 100 mV | 10 MΩ ± 2%, >10 GΩ | 6 + 5 | 27 + 7 | 28 + 8 | 3 + 2 | 0.3 + 1 |
| 1 V | 4.5 + 0.8 | 15 + 2.5 | 18 + 2.5 | 2 + 0.2 | 0.3 + 0.1 | |
| 10 V | 2 + 0.5 | 10.5 + 0.5 | 12 + 0.5 | 0.3 + 0.02 | 0.3 + 0.01 | |
Table 1: PXIe-4081 DMM Specifications
The following equation helps calculate the DMM’s accuracy worst case scenario:
Accuracy = ± (A/1,000,000) x reading + (B/1,000,000) x range
A = ppm of reading component
B = ppm of range component
Note: add 2 uV if nulling is not used
Based on the voltage drop we are measuring (10 uV), we will consider the specifications for the 100 mV range. Using the previous formula, we can estimate the DMM’s voltage measurement accuracy. Assuming that the DMM was self-calibrated within 90 days of the measurement, we can use the following numbers:
ppm of reading = 27
ppm of range = 7
Range = 100 mV
Expected signal = 10 uV
Accuracy = 700 nV + 2 uV = 2.7 uV
Knowing that the instrument accuracy is ±2.7 uV, we can calculate accuracy of the current reading by using Ohm’s Law, the instrument’s accuracy, and sense resistor error:
Ohm's Law = I = V/R
Measurement error = ± 2.7 uV/100 mΩ = ± 27 uA
Total error = measurement error + sense resistor error = ± 27 uA + 100 nA = ± 27.1 uA
Power consumption error = 2.7 uV x 27.1 uA = 73.17 pW
As we observe from these equations, using a 1% tolerance resistor, the sense resistor error becomes negligible. As a result, the system setup can measure 100 uA current consumption in the lowpower state within an accuracy of 27 uA without even using DC nulling. The accuracy could be improved simply by applying this technique.
Using Oscilloscopes for Low-Power Readings
Oscilloscopes are the second type of instrument often used for power measurements. Given their wide bandwidth and high sampling rates, oscilloscopes are often the preferred instrument to characterize dynamic changes in power consumption of a device. For illustrative purposes, let’s use the NI PXIe-5163 oscilloscope with a 1 GS/s sampling rate, 200 MHz, and a 14-bit resolution.
| Accuracy | |
|---|---|
| Resolution | 14 bits |
| DC accuracy4,5 | |
| 50 Ω | ± [(0.5% x |Reading|) + (0.2% of FS)] , warranted |
| 1 MΩ | ± [(0.65% x |Reading-Vertical Offset|) + (0.2% of FS) + 0.15 mV] , warranted |
| DC drift6 | ± 0.0013 dB per °C at 50 kHz |
| AC amplitude accuracy4 | ± 0.225 dB at 50 kHz, warranted |
Table 2: PXIe-5163 Oscilloscope Specifications
Calculating an oscilloscope’s accuracy worst-case scenario is a function of input range and vertical offset. For this calculation, we’ll use a 1-MΩ internal resistance because it is better suited for measuring low voltage. In this example, we’ll evaluate voltage drop across a sense resistor in a low-power mode with voltage reading of 10 uV. With this measurement, we will use vertical offset of 0 and full-scale input range of 0.25 V. The equation to calculate the accuracy is taken directly from the specifications document, as shown in Figure 3:
Accuracy = ± [(0.65% x |Reading - Vertical Offset|) + (0.4% x |Vertical offset|) + (0.2% of FS) + 0.15 mV]
Accuracy = ± [(0.65% x |(10 uV - 0 V)|) + (0.4% x |0 V|) + (0.2% x .25 V) + 0.15 mV] = ± 650.01 uV
Note that DC/DC drift also needs to be accounted for when the board temperature of the device is more than ±3 °C since its last calibration, as noted in the specifications document. Because temperature varies from device to device, we won’t take it into consideration and assume less than ±3 °C. Note that the vertical offset is provided in the specifications in Table 3.
Knowing that the instrument accuracy is ±650 uV, we can calculate accuracy of current reading by using Ohm’s Law, the instrument’s accuracy, and sense resistor error:
Ohm's Law = I = V/R
Measurement error = ± 650.01 uV/100 mΩ = ± 6.5 mA
Total error = measurement error + sense resistor error = ± 6.5 mA + 100 nA = ± 6.5 mA
Power consumption error = 650 uV x 6.5 mA = 4.23 uW
From the previous equation, we can observe that the currentmeasurement accuracy of the system using the oscilloscope would yield a current-measurement accuracy of only 6.5 mA, which would be insufficient to accurately measure the low-powerstate current consumption of 100 uA. However, the oscilloscope could accurately measure the power consumption of the device in active state within a reasonable level of accuracy and is often used to characterize transient power consumption behaviors of an active device.
DAQ Devices for Low-Power Measurements
DAQ devices are often used to acquire voltage and/or data on multiple channels. Although some might consider DAQ devices as a low-cost measurement tool, some of the higher-end models also deliver excellent DC measurement accuracy. For illustrative purposes, we’ll consider two DAQ devices. The first one, the PXI-6289, is a 32 AI (18-bit, 625 kS/s), 4 AO, and 48 DIO module. Like the previous examples, the following accuracy calculations will solve for worst-case scenario, which is measuring power consumption in the device’s low-power mode. Using Table 3, we can calculate DC accuracy using the equation from the following specifications document.
| Nominal Range Positive Full Scale | Nominal Range Negative Full Scale | Residual Gain Error (ppm of Reading) | Residual Offset Error (ppm of Range) | Offset Tempco (ppm of Range/°C) | Random Noise (UVRMS) | Absolute Accuracy at Full Scale (UV) | Sensitivity (UV) |
|---|---|---|---|---|---|---|---|
| 10 | -10 | 40 | 8 | 11 | 60 | 980 | 24 |
| 5 | -5 | 45 | 8 | 11 | 30 | 510 | 12 |
| 2 | -2 | 45 | 8 | 13 | 12 | 210 | 4.8 |
| 1 | -1 | 55 | 15 | 15 | 7 | 120 | 2.8 |
| 0.5 | -0.5 | 55 | 30 | 20 | 4 | 70 | 1.6 |
| 0.2 | -0.2 | 75 | 45 | 35 | 3 | 39 | 1.2 |
| 0.1 | -0.1 | 120 | 60 | 60 | 2 | 28 | 0.8 |
Table 3: PXI-6289 Accuracy Table from Specifications Document
Absolute accuracy = (Reading x Gain error) + (Range x Offset error) + Noise uncertainty
Using absolute accuracy, the “reading” will be voltage drop across sense resistor (10 uV). In addition, we will use the smallest input range possible (0.1 V). Note that gain error and offset error are derived using additional calculations. When calculating gain and offset error, we will assume 5 °C between last calibration and gain temperature coefficient (gain tempco) of 17 ppm/°C, reference tempco of 1 ppm/°C, and INL error 10 ppm of range.
Gain error = Residual AI gain error + Gain tempco x Temperature change from last internal calibration + Reference tempco x Temperature change from last internal calibration
Offset error = Residual offset error + Offset tempco x Temperature change from last internal calibration + INL error noise uncertainty
Noise uncertainty = random noise x 3/√100
Gain error = 120 ppm + (17 ppm x 5) + (1 ppm x 5) = 210 ppm
Offset error = (60 ppm + (60 ppm x 5)) + 10 ppm = 372 ppm
Noise uncertainty = 9 uV x 3/√100 = 2.7 uV
Absolute accuracy = 0.1 V x (210 ppm) + 0.1 V x (372 ppm) + 2.7 uV = 60.7 uV
After adding up all the possible errors, this instrument’s DC accuracy is 60.7 uV. Now, we can calculate accuracy of the current reading by using Ohm’s law, the instrument’s accuracy, and sense resistor error:
Ohm's Law = I = V/R
Measurement error = ± 60.7 uV/100 mΩ = ± 607 uA
Total error = measurement error + sense error = ± 607 uA + 100 nA = ± 607 uA
Power consumption error = 60.7 uV x 607 uA = 36.85 nW
Applying this calculation to the circuit in Figure 1, we can see that this specific DAQ device can measure current accuracy to within ±1 mA of the actual current consumption. Thus, although the device might be sufficient to characterize power consumption in the devices’ active state (1 A), it lacks the accuracy to measure current consumption in low-power mode (100 uA).
Higher-Performance DAQ Device
By contrast, we can compare the performance of the above multifunction DAQ device with a higher-performance end model. In our second DAQ device comparison, we’ll evaluate the performance of NI’s PXIe-4309. This device has a sample rate of up to 2 MS/s, 28-bit flexible resolution, 32 channels, and ±15 V input range.
Similar to the DMM, the NI PXIe-4309 uses additional accuracy techniques such as auto zero, chopping, and offset to improve DC measurement accuracy. To best illustrate the benefits that PXIe-4309’s additional functionalities bring, let’s evaluate an example where we enable auto zero, but offset null is not considered at the start of the acquisition. In this case, auto-zero sampling adds the most significant improvement when reading low voltages, and offset nulling removes the largest source of error being offset error with 4.5 uV when reading low voltages. Because our reading is 10 uV, the offset nulling feature is not required. For now, we’ll continue using the smallest range in Table 4 (0.1 V).
| Range | Absolute Accuracy*, **, †† | Temperature Coefficient †† | ||
|---|---|---|---|---|
24 Hour †, ‡ TEXTCAL ± 1 °C, TSELFCAL ± 1 °C | 2 Year TEXTCAL ± 5 °C, TSELFCAL ± 1 °C | 2 Year TEXTCAL ± 10 °C, TSELFCAL ± 5 °C | 0 °C - 55 °C | |
| ± (ppm of Reading + UV) / °C | ± (ppm of Reading + UV) / °C | |||
| 0.1 V | 33 + 0.3 | 60 + 4.7 | 165 + 5.1 | 25 + 0.1 |
| 1.0 V | 28 + 0.5 | 55 + 9.3 | 140 + 9.7 | 20 + 0.1 |
| 10 V | 23 + 2.7 | 50 + 55.4 | 115 + 55.8 | 15 + 0.1 |
| 15 V | 28 + 4.0 | 55 + 156.1 | 140 + 156.5 | 20 + 0.1 |
*Source Impedance ≤ 50Ω †Relative to External Calibration Source ‡Assumes Offset Nulling **Sample Rate ≤ S/s
††Temperature Coefficient is an adder to the Absolute Accuracy values that does not apply unless operating outside of the stated self-calibration temperature intervals.
Temperature Coefficient is included in the absolute Accuracy values over the stated self-calibration temperature intervals.
Table 4: PXIe-4309 Accuracy Table from Specifications Document
As mentioned earlier, one of the largest sources of error from the DAQ device is the offset error. In this case, we’ll consider the scenario of a two-year calibration cycle with a 0.1 V voltage range. In this example, a quick accuracy assumption can be determined by looking at the specifications document in Table 5. The offset portion of the total error is 4.7 uV with two-year calibration. An equation for offset error can be calculated using linearity, noise, and residual offset, which are found in the specifications document (Table 6). The following equations help to calculate the overall accuracy of the device:
Offset error = residual offset + linearity
Linearity error = 5 ppm in 100 mV range = 5/1,000,000 = 0.0000005 V
Residual offset = 4 uV
Noise = Noise (RMS) x √2 = 0.00000054 V
Gain error = 60 ppm = (60/1,000,000 = 0.00006)
Accuracy: offset error + noise + gain error
Based on the voltage drop we are measuring (10 uV), we will consider the same specifications for the 100-mV range as before. Assuming the PXIe-4309 was calibrated within two years of the measurement, we can use the following figures:
Offset error = 4.5 uV (account for this with nulling with less 5 °C)
Linearity = 0.1 V x 5 ppm = 500 nV
Residual offset = 4 uV
Noise = 20 nVrms x 1.414213562 = 28 nV peak to peak
Gain error = 10 uV x 60 ppm = 600 pV
Accuracy = 4.7 uV + 28 nV + 600 pV = 4.73 uV
After adding all the possible errors, the DC accuracy without nulling for PXIe-4309 is 4.73 uV while sampling at 10 samples per second. Like the previous examples, let’s calculate accuracy of the current reading by using Ohm’s Law, the instrument’s accuracy, and sense resistor error:
Ohm's Law = I = V/R
Measurement error = ± 4.73 uV/100 mΩ = ± 47.3 uA
Total error = measurement error + sense resistor error = ± 47.3 uA + 100 nA = ± 47.4 uA
Power consumption error = 4.7 uV x 47.4 uA = 222.78 pW
Based on the calculations above, we can determine that the PXIe-4309 DAQ device can measure current consumption within an accuracy of within ±47.5 uA, without correcting for offset nulling. Note that DC offset is a significant portion of the overall measurement error. Thus, even basic nulling techniques could improve the accuracy of this measurement substantially, even resulting in accuracy performance of better than ±1 uA, using the previous measurement configuration.
Evaluating the Instruments to Find the Right Fit for Low-Power Validation
As mentioned previously, accuracy is one of the most important considerations when evaluating instruments for low-voltage measurements along with features like the fast-sampling rate data capture for dynamic signals. Beyond that, additional channels provide the adaptability to measure multiple power rails. The overall results showed that although most instruments are equipped for voltage readings, there is a significant variance of accuracy. First, DMMs would be able to accurately read active- and low-power modes. Second, the oscilloscope is best-suited for capturing dynamic signals due to their high sampling rate. Third, DAQ PXI-6289 would be sufficient to read active-power mode but would not be sufficient to measure low-power mode. Finally, the PXIe-4309 would be able to accurately measure both the active- and low-power mode needed in Figure 1.
| Instrument | Measurement Accuracy |
|---|---|
| DMM (PXIe-4081) | High precision low voltage measurements with instruments accuracy of ± 73.17 pW (2.7 uV) |
| Oscilloscope (PXIe-5163) | Low voltage measurements with instruments accuracy of ± 4.23 uW (650 uV) |
| DAQ Device (PXI-6289) | Low voltage measurements with instruments accuracy of ± 35.45 nW (60.7 uV) |
| DAQ Device (PXIe-4309) | Low voltage measurements with instruments accuracy of ± 222.78 pW (4.74 uV) |
Table 5: Comparison of Each Instrument’s Performance Based on the Low-Power Measurement Requirements
Choosing the right tool to measure low power leads to more accurate power validation—which, in turn, enhances product performance. In a market where consumers expect their electronic devices to stay powered on longer with a single charge, selecting high-performance instrumentation like the PXIe-4309 can help quickly and effectively validate your device’s power consumption. Overall, the PXIe-4309 analog input module outperforms oscilloscopes and comparable DAQ devices. It even matches the performance of a 7½-digit DMM for measuring current on these low-ohm shunt resistors. With a higher channel count, PXIe-4309 provides enough measurement density for requirements of modern power validation in complex electronic designs.