Home Shop What is LabVIEW? Patented Order-Tracking Algorithm

Patented Order-Tracking Algorithm

Updated Jul 8, 2024

Overview

With the state-of-the-art Gabor order-tracking algorithm, you can analyze sound, vibration, and other dynamic signals from mechanical systems with rotating components. Using the patented algorithm, based on the principles of joint time-frequency analysis (JTFA), you can build custom measurement and automation applications that include order analysis, tracking, and extraction.

Contents

System Overview

The typical system for National Instruments order analysis applications include the following components:

 
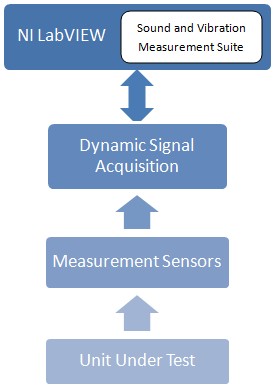
Of the above components, NI provides products for measuring vibration and sound.
 
Back to top

Sound and Vibration Measurement Suite

With the state-of-the-art Gabor order-tracking algorithm, you can analyze sound, vibration, and other dynamic signals from mechanical systems with rotating components. Using the patented algorithm, based on the principles of joint time-frequency analysis (JTFA), you can build custom measurement and automation applications that include order analysis, tracking, and extraction.

 
Figure 1: The LabVIEW Sound and Vibration Measurement Suite helps you quickly create powerful Sound and Vibration applications
 
The basic technique of order analysis involves obtaining the instantaneous speed of the rotating shaft of a machine from a tachometer or encoder signal. The speed is then correlated to the noise or vibration signal produced by the machine to obtain information about the order components such as waveforms, magnitudes, and phases. In order analysis, we focus on revolutions, rather than time, as the basis for signal analysis. Thus, in the spectrum domain, the focus is on orders rather than frequency components. Currently, methods used to perform order analysis include resampling, adaptive filters, and the Gabor transform. The LabVIEW Sound and Vibration Measurement Suite employs the Gabor transform method of order analysis and patented order-tracking algorithm to ensure perfect reconstruction of the original time-domain signal. Guaranteeing perfect reconstruction of the time signal is critical for proper diagnosis of rotating machinery, thus making the Sound and Vibration Suite a powerful tool for monitoring the condition of machinery.
Back to top

The Gabor Transform

The Gabor transform is one of the invertible joint time-frequency transforms. This means that any time-domain input signal, or an approximation thereof, can be recovered from its transform result by applying an inverse Gabor transform. The transform result is called a Gabor coefficient, and the inverse Gabor transform is known as Gabor expansion.

The Gabor expansion, a mathematical tool, characterizes a signal jointly in the time and frequency domains. Although Nobel laureate Dennis Gabor introduced the Gabor expansion more than half a century ago, its implementation had been an open research topic until Bastiaans discovered the relationship between the Gabor expansion and the short-time Fourier transform (STFT) in the early 1980s. Over the years, many different implementation schemes for the discrete Gabor expansion have been proposed. The one employed in the LabVIEW Sound and Vibration Measurement Suite is an extension of the method originally developed by Wexler and Raz. In this method, lengths of the analysis and synthesis window functions are the same, while perfect reconstruction is guaranteed. Using the Gabor transform and patented order-tracking algorithm for analysis of rotating machinery is a powerful tool for machinery monitoring and asset management programs. Using this unique measurement, the Gabor transform with patented order tracking, provides a better solution for the following reasons:

  • Transform-based technique does not introduce phase or amplitude distortion into the extracted signal. The lack of such distortion means that you can directly perform trace math operations with your original signal and any extracted orders. For example, you can directly attenuate or amplify order-related components of your original signal.
  • Intermediate step of order energy specification occurs in the time-frequency domain. This domain offers an intuitive, visual perspective in which signal energy appears as a function of frequency and time. Order energy is visible as distinct lines in this domain which you can interactively or automatically select. By performing the inverse Gabor transform, you can retrieve the time or frequency-domain representations of whatever you select.
  • Flexible order selection. The Sound and Vibration Measurement Suite includes high-level VIs and pre-built examples for order extraction that select order energy with either a constant bandwidth or with a bandwidth that varies with the rate of speed change. With speed-varying order energy specification, you won’t miss energy associated with widening bandwidth that goes with more rapid speed changes. Because you can select any portion of the Gabor joint time-frequency representation of your signal, you are also free to build your own custom selection technique. The Sound and Vibration Measurement Suite also includes LabVIEW VIs with which you can arbitrarily specify a selection mask that designates what energy to retrieve from the original signal.
Back to top