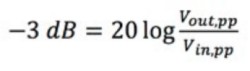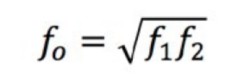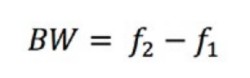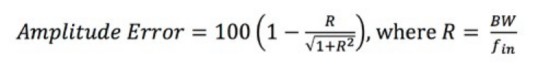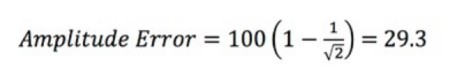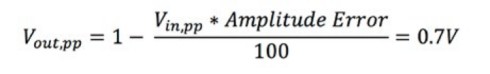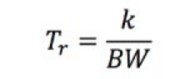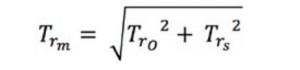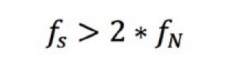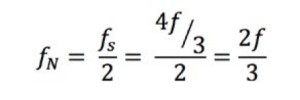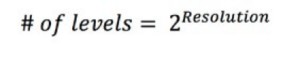Acquiring an Analog Signal: Bandwidth, Nyquist Sampling Theorem, and Aliasing

Scientists and engineers often use a digitizer to capture analog data in the real world and convert it into digital signals for analysis. A digitizer is any device used to convert analog signals into digital signals. One of the most common digitizers is a cell phone, which converts a voice, an analog signal, into a digital signal to send to another phone. However, in test and measurement applications, a digitizer most often refers to an oscilloscope or a digital multimeter (DMM). This article focuses on oscilloscopes, but most topics are also applicable to other digitizers.

Regardless of the type, the digitizer is vital for the system to accurately reconstruct a waveform. To ensure you select the correct oscilloscope for your application, consider the bandwidth, sampling rate, and resolution of the oscilloscope. 

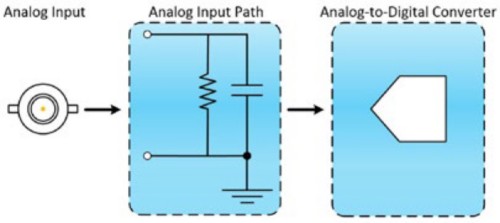
The front end of an oscilloscope consists of two components: an analog input path and an analog-to-digital converter (ADC). The analog input path attenuates, amplifies, filters, and/or couples the signal to optimize it in preparation for digitization by the ADC. The ADC samples the conditioned waveform and converts the analog input signal to digital values that represent the analog input waveform. The frequency response of the input path causes an inherent loss of amplitude and phase information.

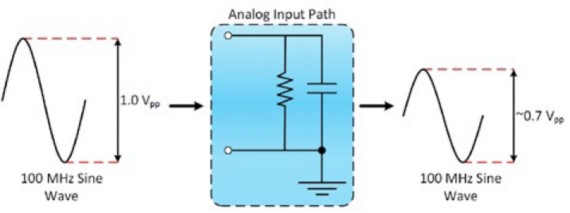
Bandwidth describes the analog front end’s ability to get a signal from the outside world to the ADC with minimal amplitude loss—from the tip of the probe or test fixture to the input of the ADC. In other words, the bandwidth describes the range of frequencies an oscilloscope can accurately measure.

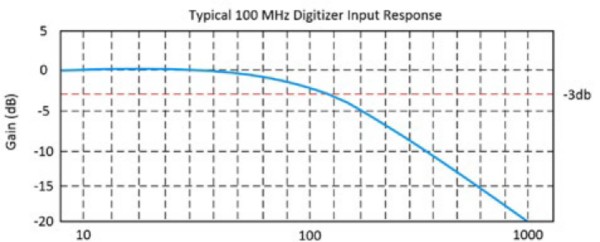
It is defined as the frequency at which a sinusoidal input signal is attenuated to 70.7 percent of its original amplitude, which is also known as the -3 dB point. Figures 2 and 3 show the typical input response for a 100 MHz oscilloscope.

^{Figure 1: Bandwidth describes the frequency range in which the input signal can pass through the oscilloscope front end, which is made of two components: an analog input path and an ADC.}

^{Figure 2: Bandwidth is when the input signal is attenuated to 70.7 percent of its original amplitude.}  

^{Figure 3: This graph indicates that at 100 MHz, the input signal hits the -3dB point.}  

Bandwidth is measured between the lower and upper frequency points where the signal amplitude falls to -3 dB below the passband frequency. This sounds complicated, but when you break it down it is actually relatively easy. 

First, you want to calculate your -3 dB value.

^{Equation 1: Calculating the -3 dB Point.}

V_in,pp is the peak-to-peak voltage of the input signal, and V_out,pp is the peak-to-peak voltage of the output signal. For example, if you apply the formula shown in Equation 1, V_out,pp would be approximately equal to 0.7 V.

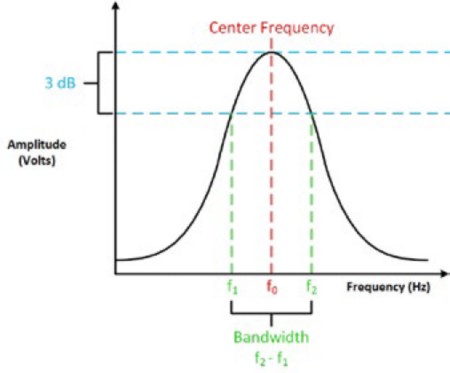
Because the input signal is a sine wave, there are two frequencies at which the output signal hits this voltage; these are called the corner frequencies f₁ and f₂. These two frequencies go by many different names such as corner frequency, cut-off frequency, crossover frequency, half-power frequency, 3 dB frequency, and break frequency. However, all these terms refer to the same values. The center frequency, f₀, of the signal is the geometric mean of f₁ and f₂.

^{Equation 2: Calculating the Center Frequency.}

You can calculate the bandwidth (BW) by subtracting the two corner frequencies. 

^{Equation 3: Calculating the Bandwidth} 

^{Figure 4: The bandwidth, the corner frequency, the center frequency, and the 3 dB point are all connected.}

Calculating Amplitude Error

Another equation that is often helpful is for amplitude error.  

^{Equation 4: Calculating the Amplitude Error.}

The amplitude error is expressed as a percentage, and R is the ratio of the oscilloscope’s bandwidth to the input signal frequency (f_in).

Using the example above, you have a 100 MHz oscilloscope with a 100 MHz sine wave input signal at 1 V, and BW = 100 MHz and (f_in) = 100 MHz. This means R = 1. Then you just have to solve the equation:

The amplitude error is 29.3 percent. You can then determine the output voltage for the 1 V signal:

It is recommended that the bandwidth of your oscilloscope be three to five times the highest frequency component of interest in the measured signal to capture the signal with minimal amplitude error. For instance, for the 1 V sine wave at 100 MHz, you should use an oscilloscope with 300 MHz to 500 MHz bandwidth. The amplitude error of a 100 MHz signal at these bandwidths are:

Calculating Rise Time

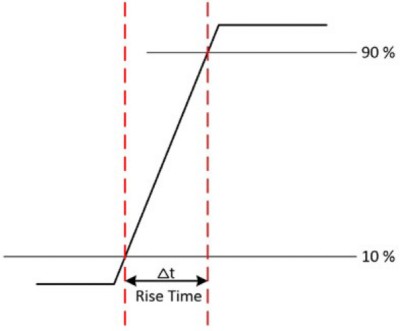
An oscilloscope must have the appropriate bandwidth to accurately measure the signal, but it must also have sufficient rise time to accurately capture the details of rapid transitions. This is most applicable if measuring digital signals such as pulses and steps. The rise time of an input signal is the time for a signal to transition from 10 percent to 90 percent of the maximum signal amplitude. Some oscilloscopes may use 20 percent to 80 percent, so be sure to check your user manual.

^{Figure 5: The rise time of an input signal is the time for a signal to transition from 10 percent to 90 percent of the maximum signal amplitude.}

The rise time (Tr) can be calculated as follows:

^{Equation 5: Calculating the Rise Time.}

The constant k is dependent on the oscilloscope. Most oscilloscopes with a bandwidth less than 1 GHz typically have k = 0.35, while oscilloscopes with a bandwidth greater than 1 GHz usually have a value of k between 0.4 and 0.45.

The theoretical rise time , T_r-m, can be calculated from the rise time of the oscilloscope T_r-o and the actual rise time of the input signal, T_r-s, using the following formula.

^{Equation 6: Calculating the Theoretical Rise Time Measured.}

It is recommended that the rise time of the oscilloscope be one-third to one-fifth the rise time of the measured signal to capture the signal with minimal rise time error.

The sample rate, also referred to as sampling rate, is not directly related to the bandwidth specification. Sample rate is the frequency at which the ADC converts the analog input waveform to digital data. The oscilloscope samples the signal after any attenuation, gain, and/ or filtering has been applied to the analog input path and converts the resulting waveform to digital representation. It does so in snapshots, similar to the frames of a movie. The faster the oscilloscope samples, the greater the resolution and detail that can be seen in the waveform. 

Nyquist Sampling Theorem

The Nyquist Sampling Theorem explains the relationship between the sample rate and the frequency of the measured signal. It states that the sample rate f_s must be greater than twice the highest frequency component of interest in the measured signal. This frequency is often referred to as the Nyquist frequency, f_N. 

^{Equation 7: The sample rate should be greater than twice the Nyquist frequency.} 

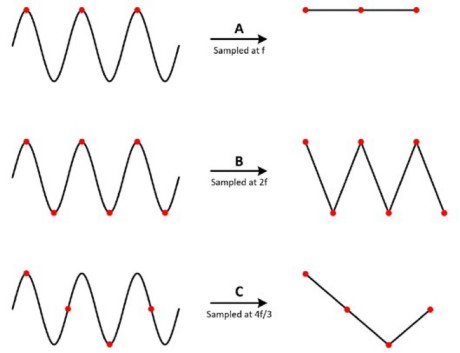
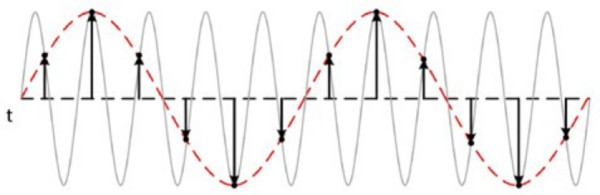
To understand why, take a look at a sine wave measured at different rates. In case A, the sine wave of frequency f is sampled at that same frequency. Those samples are marked on the original signal on the left and, when constructed on the right, the signal incorrectly appears as a constant DC voltage. In case B, the sample rate is twice the frequency of the signal. It now appears as a triangle waveform. In this case, f is equal to the Nyquist frequency, which is the highest frequency component allowed to avoid aliasing for a given sampling frequency. In case C, the sampling rate is at 4f/3. The Nyquist frequency in this case is:

Because f is larger than the Nyquist frequency, this sample rate reproduces an alias waveform of incorrect frequency and shape.

Thus, to accurately reconstruct the waveform, the sample rate fs must be greater than twice the highest frequency component of interest in the measured signal. Usually, you want to sample around five times greater than the signal frequency.

^{Figure 6: Too low a sample rate can cause inaccurate reconstruction of the waveform.} 

Aliasing

If you need to sample at a certain rate to avoid aliasing, then what exactly is aliasing? If a signal is sampled at a sampling rate smaller than twice the Nyquist frequency, false lower frequency components appear in the sampled data. This phenomenon is referred to as aliasing. The following figure shows an 800 kHz sine wave sampled at 1 MS/s. The dotted line indicates the aliased signal recorded at that sample rate. The 800 kHz frequency aliases back in the passband, falsely appearing as a 200 kHz sine wave.

^{Figure 7: Aliasing occurs when a sample rate is too low and reproduces an inaccurate waveform representation.} 

The alias frequency f_a can be calculated to determine how an input signal at a frequency over the Nyquist frequency appears. It is the absolute value of the closest integer multiple of the sample frequency minus the frequency of the input signal. 

^{Equation 8: Calculating the Alias Frequency.}

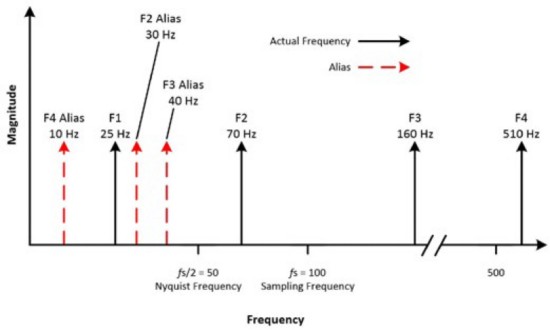
For example, consider a signal with a sample frequency of 100 Hz, and the input signal contains the following frequencies: 25 Hz, 70 Hz, 160 Hz, and 510 Hz. Frequencies below the Nyquist frequency of 50 Hz are sampled correctly; those over 50 Hz appear as alias. 

^{Figure 8: Different frequency values are measured, some of which are alias frequencies and some of which are actual frequencies from the waveform.}

Here are the calculations for the alias frequencies: 

In addition to increasing the sample rate, aliasing can also be prevented by using an antialiasing filter. This is a lowpass filter that attenuates any frequencies in the input signal that are greater than the Nyquist frequency, and must be introduced before the ADC to restrict the bandwidth of the input signal to meet the sampling criteria. Analog input channels can have both analog and digital filters implemented in hardware to assist with aliasing prevention.

Another factor to consider when selecting an oscilloscope for an application is the resolution. Bits of resolution refers to the number of unique vertical levels that an oscilloscope can use to represent a signal. One way to understand the concept of resolution is by comparison with a yardstick. Divide a meter yardstick into millimeters; what is the resolution? The smallest tick on the yardstick is the resolution–or 1 out of 1,000.

The resolution of an ADC is a function of how many parts the maximum signal can be divided into. The amplitude resolution is limited by the number of discrete output levels an ADC has. A binary code represents each division; as such, the number of levels can be calculated as follows:

^{Equation 9: Calculating the Discrete Output Levels of an ADC.}

For example, a 3-bit oscilloscope has 23 or eight levels. A 16-bit oscilloscope on the other hand has 216 or 65,536 levels. The minimum detectable voltage change or code width can be calculated as follows:

^{Equation 9: Calculating the Discrete Output Levels of an ADC.}

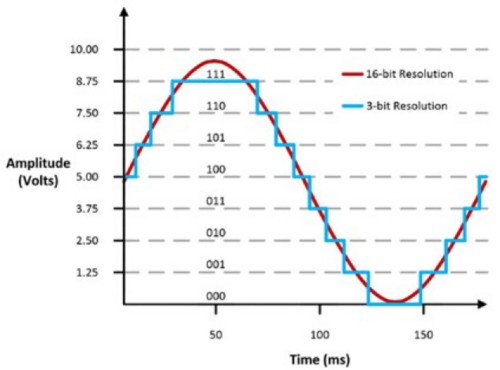
The code width is also referred to as the least significant bit (LSB). If the device input range is 0 to 10 V, then a 3-bit oscilloscope has a code width of 10/8 = 1.25 V while a 16-bit oscilloscope has a code width of 10/65,536 = 305 μV. This can mean a big difference in how the signal is displayed.

^{Figure 9: Difference of a Waveform Between 16 Bits and 3 Bits of Resolution.}

The resolution you need depends on your application; the higher the resolution, the more the oscilloscope costs. Keep in mind that an oscilloscope with high resolution doesn’t necessarily mean that it has high accuracy. However, the achievable accuracy of an instrument is limited by the resolution. Resolution limits the precision of a measurement; the higher the resolution (number of bits), the more precise the measurement.

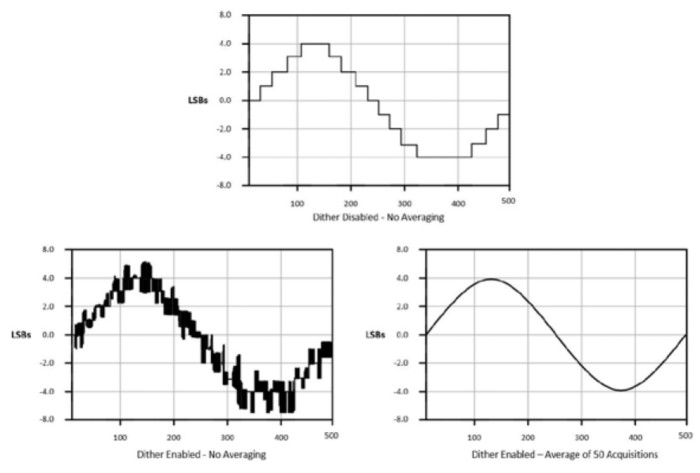
Some oscilloscopes use a method called dithering to help smooth out signals to get the appearance of a higher resolution. Dithering involves the deliberate addition of noise to the input signal. It helps by smearing out the little differences in amplitude resolution. The key is to add random noise in a way that makes the signal bounce back and forth between successive levels. Of course, this in itself just makes the signal noisier. But, the signal smoothes out by averaging this noise digitally once the signal is acquired.

^{Figure 10: Dithering can help smooth out a signal.} 

• Bandwidth describes the range of frequencies an oscilloscope can accurately measure. It is defined as the frequency at which a sinusoidal input signal is attenuated to 70.7 percent of its original amplitude, which is also known as the -3 dB point.
• Bandwidth is the difference between the corner frequencies.
• Amplitude error is a percentage that is the ratio of the bandwidth to the input signal frequencies that assists with determining the noise in a system.
• It is recommended that the bandwidth of your oscilloscope be three to five times the highest frequency component of interest in the measured signal to capture the signal with minimal amplitude error.
• The rise time of an input signal is the time for a signal to transition from 10 percent to 90 percent of the maximum signal amplitude.
• It is recommended that the rise time of the oscilloscope be one-third to one-fifth the rise time of the measured signal to capture the signal with minimal rise time error.
• Sample rate is the frequency at which the ADC converts the analog input waveform to digital data.
• The sample rate should be at least twice the highest frequency of interest in the signal, but most of the time should be around five times greater.
• Aliasing is when false frequency components appear in sampled data.
• Bits of resolution refers to the number of unique vertical levels that an oscilloscope can use to represent a signal.
• The higher the resolution of an instrument, the greater the precision.

• Download all instrument fundamentals content