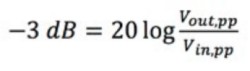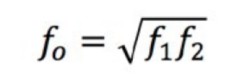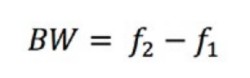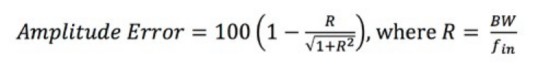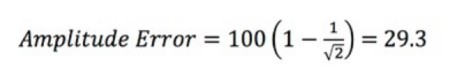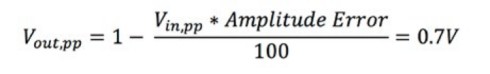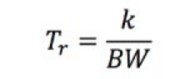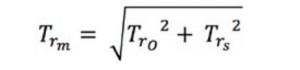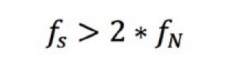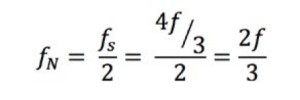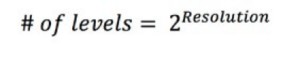Erfassen eines Analogsignals: Bandbreite, Nyquist-Abtasttheorem und Aliasing

Wissenschaftler und Ingenieure verwenden oft einen Digitizer, um Analogdaten in der realen Welt zu erfassen und in Digitalsignale für die Analyse umzuwandeln. Ein Digitizer ist jedes Gerät, mit dem Analogsignale in Digitalsignale umgewandelt werden. Einer der gängigsten Digitizer ist ein Mobiltelefon, das eine Stimme, ein Analogsignal, in ein Digitalsignal umwandelt, um es an ein anderes Telefon zu senden. In Test- und Messanwendungen ist ein Digitizer jedoch meist ein Oszilloskop oder ein Digitalmultimeter (DMM). Dieser Artikel befasst sich mit Oszilloskopen, aber die meisten Themen sind auch auf andere Digitizer anwendbar.

Unabhängig vom Typ ist der Digitizer für die genaue Rekonstruktion eines Signalverlaufs entscheidend. Um sicherzustellen, dass Sie das richtige Oszilloskop für Ihre Anwendung auswählen, sollten Sie die Bandbreite, Sample-Rate und Auflösung des Oszilloskops berücksichtigen. 

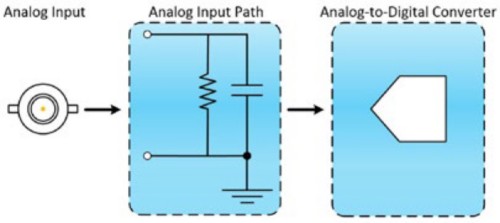
Das Frontend eines Oszilloskops besteht aus zwei Komponenten: einem analogen Eingangspfad und einem Analog/Digital-Wandler (A/D-Wandler). Der analoge Eingangspfad dämpft, verstärkt, filtert und/oder koppelt das Signal, um es für die Digitalisierung durch den A/D-Wandler zu optimieren. Der A/D-Wandler tastet den aufbereiteten Signalverlauf ab und wandelt das analoge Eingangssignal in digitale Werte um, die den analogen Eingangssignalverlauf darstellen. Der Frequenzgang des Eingangspfads führt zu einem inhärenten Verlust von Amplituden- und Phaseninformationen.

Bandbreite beschreibt die Fähigkeit des analogen Frontends, ein Signal von der Außenwelt mit minimalem Amplitudenverlust an den A/D-Wandler zu übertragen – von der Spitze der Sonde oder der Testvorrichtung bis zum Eingang des A/D-Wandlers. Die Bandbreite beschreibt also den Frequenzbereich, den ein Oszilloskop genau messen kann.

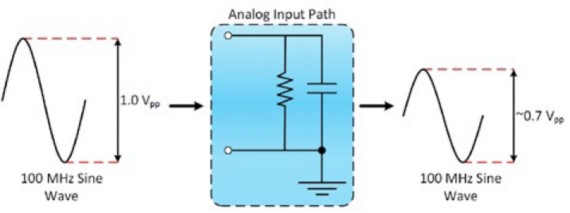
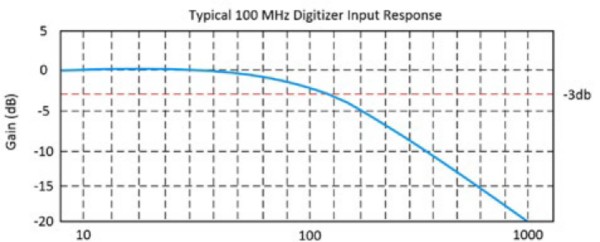
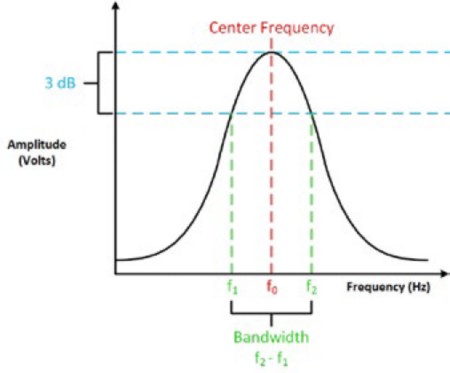
Sie wird als die Frequenz definiert, bei der ein sinusförmiges Eingangssignal auf 70,7 Prozent seiner ursprünglichen Amplitude gedämpft wird, was auch als „-3 dB“-Punkt bezeichnet wird. Abbildungen 2 und 3 zeigen das typische Eingangsverhalten eines 100-MHz-Oszilloskops.

^{Abbildung 1: Bandbreite beschreibt den Frequenzbereich, in dem das Eingangssignal das Oszilloskop-Frontend passieren kann, das aus zwei Komponenten besteht: einem analogen Eingangspfad und einem A/D-Wandler.}

^{Abbildung 2: Bandbreite ist, wenn das Eingangssignal auf 70,7 Prozent seiner ursprünglichen Amplitude gedämpft wird.}

^{Abbildung 3: Dieser Graph zeigt, dass das Eingangssignal bei 100 MHz den -3 dB-Punkt erreicht.}

Die Bandbreite wird zwischen den unteren und oberen Frequenzpunkten gemessen, bei denen die Signalamplitude auf -3 dB unter die Durchlassfrequenz fällt. Das klingt kompliziert, ist aber in einer schrittweisen Anleitung leicht zu verstehen. 

Zuerst müssen Sie Ihren -3 dB-Wert berechnen.

^{Gleichung 1: Berechnung des -3 dB-Punkts.}

V_in,pp ist die Spitze-Spitze-Spannung des Eingangssignals und V_out,pp ist die Spitze-Spitze-Spannung des Ausgangssignals. Wenn Sie beispielsweise die in Gleichung 1 gezeigte Formel anwenden, wäre V_out,pp ungefähr 0,7 V.

Da das Eingangssignal eine Sinusschwingung ist, gibt es zwei Frequenzen, bei denen das Ausgangssignal auf diese Spannung trifft, die Eckfrequenzen f₁ und f₂. Diese beiden Frequenzen haben viele verschiedene Namen wie Eckfrequenz, Grenzfrequenz, Übergangsfrequenz, Halbwertsfrequenz, 3-dB-Frequenz und Abbruchfrequenz. Alle diese Begriffe beziehen sich jedoch auf dieselben Werte. Die Mittenfrequenz f₀ des Signals ist der geometrische Mittelwert von f₁ und f₂.

^{Gleichung 2: Berechnung der Mittenfrequenz.}

Die Bandbreite (BW) kann durch Subtraktion der beiden Eckfrequenzen berechnet werden. 

^{Gleichung 3: Berechnung der Bandbreite.}

^{Abbildung 4: Bandbreite, Eckfrequenz, Mittenfrequenz und -3 dB-Punkt sind miteinander verbunden.}

Berechnung des Amplitudenfehlers

Eine weitere nützliche Gleichung ist die Gleichung für die Berechnung des Amplitudenfehlers.  

^{Gleichung 4: Berechnung des Amplitudenfehlers.}

Der Amplitudenfehler wird in Prozent ausgedrückt und R ist das Verhältnis der Bandbreite des Oszilloskops zur Eingangssignalfrequenz (f_in).

Im obigen Beispiel haben Sie ein 100-MHz-Oszilloskop mit einer 100-MHz-Sinusschwingung als Eingangssignal von 1 V, einer BW = 100 MHz und (f_in) = 100 MHz. Das bedeutet, dass R = 1 ist. Sie müssen dann lediglich die folgende Gleichung lösen:

Der Amplitudenfehler beträgt 29,3 Prozent. Sie können dann die Ausgangsspannung für das 1-V-Signal bestimmen:

Es wird empfohlen, dass die Bandbreite Ihres Oszilloskops das Drei- bis Fünffache des höchsten zu untersuchenden Frequenzanteils im gemessenen Signal beträgt, um das Signal mit minimalem Amplitudenfehler zu erfassen. Für die 1-V-Sinusschwingung bei 100 MHz sollten Sie beispielsweise ein Oszilloskop mit einer Bandbreite von 300 MHz bis 500 MHz verwenden. Amplitudenfehler eines 100-MHz-Signals bei diesen Bandbreiten sind:

Berechnung der Anstiegszeit

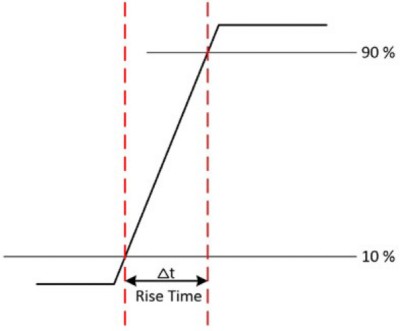
Ein Oszilloskop benötigt neben der entsprechenden Bandbreite zur genauen Messung des Signals auch eine ausreichende Anstiegszeit, um die Details von schnellen Übergängen korrekt zu erfassen. Dies gilt besonders für die Messung von Digitalsignalen wie Impulsen und Schritten. Die Anstiegszeit eines Eingangssignals ist die Zeit, in der ein Signal von 10 Prozent auf 90 Prozent der maximalen Signalamplitude übergeht. Manche Oszilloskope benötigen 20 bis 80 Prozent. Lesen Sie daher zur Sicherheit das Benutzerhandbuch.

^{Abbildung 5: Die Anstiegszeit eines Eingangssignals ist die Zeit, in der ein Signal von 10 Prozent auf 90 Prozent der maximalen Signalamplitude übergeht.}

Die Anstiegszeit (Tr) kann wie folgt berechnet werden:

^{Gleichung 5: Berechnung der Anstiegszeit.}

Die Konstante k ist vom Oszilloskop abhängig. Bei den meisten Oszilloskopen mit einer Bandbreite unter 1 GHz ist k = 0,35, während Oszilloskope mit einer Bandbreite über 1 GHz Werte von k gewöhnlich zwischen 0,4 und 0,45 aufweisen.

Die theoretische Anstiegszeit T_r-m kann aus der Anstiegszeit des Oszilloskops T_r-o und der tatsächlichen Anstiegszeit des Eingangssignals T_r-s nach folgender Formel berechnet werden:

^{Gleichung 6: Berechnung der gemessenen theoretischen Anstiegszeit.}

Es wird empfohlen, dass die Anstiegszeit des Oszilloskops ein Drittel bis ein Fünftel der Anstiegszeit des gemessenen Signals beträgt, um das Signal mit minimalem Anstiegszeitfehler zu erfassen.

Die Sample-Rate, auch Abtastrate genannt, steht in keinem direkten Zusammenhang mit der Bandbreitenspezifikation. Die Sample-Rate ist die Frequenz, mit der der A/D-Wandler den analogen Eingangssignalverlauf in digitale Daten umwandelt. Das Oszilloskop tastet das Signal nach Anwendung von Dämpfung, Verstärkung und/oder Filterung auf den analogen Eingangspfad ab und wandelt den resultierenden Signalverlauf in eine digitale Darstellung um. Dies geschieht in Form von Momentaufnahmen, ähnlich wie Bildrahmen eines Films. Je schneller das Oszilloskop abtastet, desto höher ist die Auflösung und Detailgenauigkeit des Signalverlaufs. 

Nyquist-Abtasttheorem

Mit dem Nyquist-Abtasttheorem wird der Zusammenhang zwischen der Sample-Rate und der Frequenz des gemessenen Signals beschrieben. Es gibt an, dass die Sample-Rate f_s mindestens zweimal so hoch wie der höchste zu untersuchende Frequenzanteil im gemessenen Signal sein muss. Diese Frequenz wird oft als Nyquist-Frequenz, ƒ_N, bezeichnet. 

^{Gleichung 7: Die Sample-Rate sollte mindestens zweimal so hoch wie die Nyquist-Frequenz sein.}

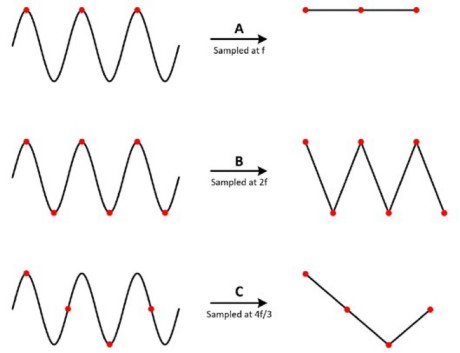
Um den Grund zu verstehen, schauen Sie sich eine mit unterschiedlichen Raten gemessene Sinusschwingung an. Im Fall A wird die Sinusschwingung der Frequenz f mit derselben Frequenz abgetastet. Diese Samples sind auf dem ursprünglichen Signal auf der linken Seite markiert. Wenn das Signal auf der rechten Seite konstruiert wird, erscheint es fälschlicherweise als konstante Gleichspannung. In Fall B ist die Sample-Rate zweimal so hoch wie Frequenz des Signals. Sie wird nun als Dreieckschwingung angezeigt. In diesem Fall ist f gleich der Nyquist-Frequenz, dem höchsten zulässigen Frequenzanteil, wenn Aliasing für eine gegebene Sample-Frequenz vermieden werden soll. Im Fall C liegt die Sample-Rate bei 4f/3. Die Nyquist-Frequenz ist in diesem Fall:

Da f größer als die Nyquist-Frequenz ist, gibt diese Sample-Rate einen Aliassignalverlauf mit falscher Frequenz und Form wieder.

Zur genauen Rekonstruktion des Signalverlaufs muss daher die Sample-Rate fs mindestens zweimal so hoch wie der höchste zu untersuchende Frequenzanteil im gemessenen Signal sein. Normalerweise soll die Sample-Rate etwa fünfmal so hoch sein wie die Signalfrequenz.

^{Abbildung 6: Eine zu niedrige Sample-Rate kann zu einer ungenauen Rekonstruktion des Signalverlaufs führen.}

Aliasing

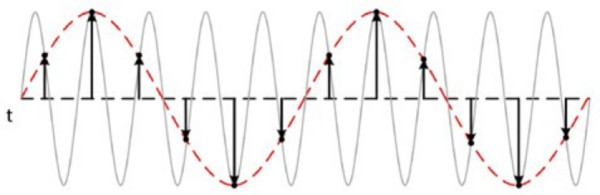
Was bedeutet es, wenn Sie zum Vermeiden von Aliasing mit einer bestimmten Rate abtasten müssen? Bei einer Sample-Rate, die nicht mindestens zweimal so hoch wie die Nyquist-Frequenz ist, erscheinen in den abgetasteten Daten falsche niedrigere Frequenzanteile. Dieses Phänomen wird als Aliasing bezeichnet. In der folgenden Abbildung sehen Sie eine mit 1 MS/s abgetastete 800-kHz-Sinusschwingung. Die gestrichelte Linie zeigt das Aliassignal an, das mit dieser Sample-Rate erfasst wird. Die 800-kHz-Frequenz wird fälschlicherweise als 200-kHz-Sinusschwingung im Durchlassbereich dargestellt.

^{Abbildung 7: Aliasing tritt auf, wenn eine Sample-Rate zu niedrig ist und eine ungenaue Signalverlaufsdarstellung reproduziert.}

Mit der berechneten Aliasfrequenz f_a kann bestimmt werden, wie ein Eingangssignal bei einer Frequenz über der Nyquist-Frequenz dargestellt wird. Sie ist der absolute Wert des nächsten ganzzahligen Vielfachen der Sample-Frequenz minus der Frequenz des Eingangssignals. 

^{Gleichung 8: Berechnung der Alias-Frequenz.}

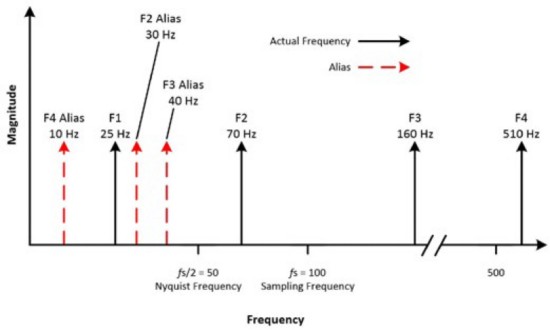
Gehen wir z. B. von einem Signal mit einer Sample-Frequenz von 100 Hz und einem Eingangssignal mit den folgenden Frequenzen aus: 25 Hz, 70 Hz, 160 Hz und 510 Hz. Die Frequenzen unterhalb der Nyquist-Frequenz von 50 Hz werden korrekt abgetastet; Frequenzen über 50 Hz werden als Alias angezeigt. 

^{Abbildung 8: Es werden unterschiedliche Frequenzwerte gemessen, von denen einige Alias-Frequenzen und einige tatsächliche Frequenzen aus dem Signalverlauf sind.}

So werden die Alias-Frequenzen berechnet: 

Neben der Erhöhung der Sample-Rate kann Aliasing auch durch einen Antialiasing-Filter verhindert werden. Dabei handelt es sich um einen Tiefpassfilter, der alle Frequenzen im Eingangssignal dämpft, die größer als die Nyquist-Frequenz sind. Der Filter muss vor dem A/D-Wandler eingesetzt werden, um die Bandbreite des Eingangssignals einzuschränken, damit die Abtastkriterien erfüllt werden. Analoge Eingangskanäle können sowohl analoge als auch digitale in der Hardware implementierte Filter haben, die beim Verhindern von Aliasing helfen.

Ein weiterer Faktor bei der Auswahl eines Oszilloskops für eine Anwendung ist die Auflösung. Die Bit-Auflösung gibt an, wie viele vertikale Pegel ein Oszilloskop zur Darstellung eines Signals verwenden kann. Das Konzept der Auflösung kann anhand eines Meterstabs veranschaulicht werden. Wenn Sie einen Meterstab in Millimeter einteilen, was ist dann die Auflösung? Die kleinste Einheit auf dem Meterstab ist die Auflösung – 1 von 1.000.

Die Auflösung eines A/D-Wandlers hängt davon ab, in wie viele Teile das maximale Signal aufgeteilt werden kann. Die Amplitudenauflösung ist durch die Anzahl der diskreten Ausgangspegel eines A/D-Wandlers begrenzt. Ein Binärcode stellt jede Division dar. Die Anzahl der Pegel kann daher wie folgt berechnet werden:

^{Gleichung 9: Berechnung der diskreten Ausgangspegel eines A/D-Wandlers.}

Ein 3-Bit-Oszilloskop hat beispielsweise 2³ oder acht Pegel. Ein 16-Bit-Oszilloskop hat dagegen 2¹⁶ oder 65.536 Pegel. Die minimal erfassbare Spannungsänderung oder Code-Breite kann wie folgt berechnet werden:

^{Gleichung 9: Berechnung der diskreten Ausgangspegel eines A/D-Wandlers.}

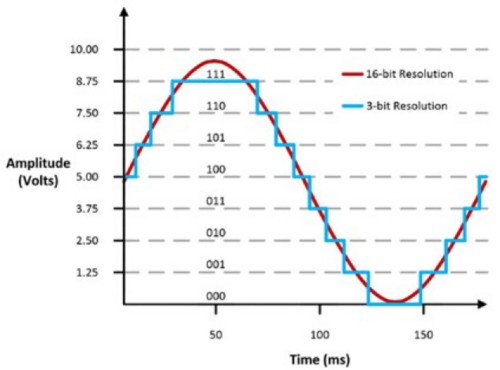
Die Code-Breite wird auch als niedrigstwertiges Bit bezeichnet. Wenn der Eingangsbereich des Geräts 0 bis 10 V ist, hat ein 3-Bit-Oszilloskop eine Code-Breite von 10/8 = 1,25 V, während ein 16-Bit-Oszilloskop eine Code-Breite von 10/65.536 = 305 μV aufweist. Das kann beim Darstellen des Signals einen großen Unterschied bedeuten.

^{Abbildung 9: Unterschied eines Signalverlaufs bei einer 16-Bit- und 3-Bit-Auflösung.}

Die benötigte Auflösung hängt von Ihrer Anwendung ab. Je höher die Auflösung, desto mehr kostet das Oszilloskop. Beachten Sie, dass ein Oszilloskop mit hoher Auflösung nicht automatisch auch eine hohe Genauigkeit erreicht. Die erreichbare Genauigkeit eines Geräts ist jedoch durch die Auflösung begrenzt. Die Auflösung schränkt die Genauigkeit einer Messung ein. Je höher die Auflösung (Anzahl Bits), desto genauer ist die Messung.

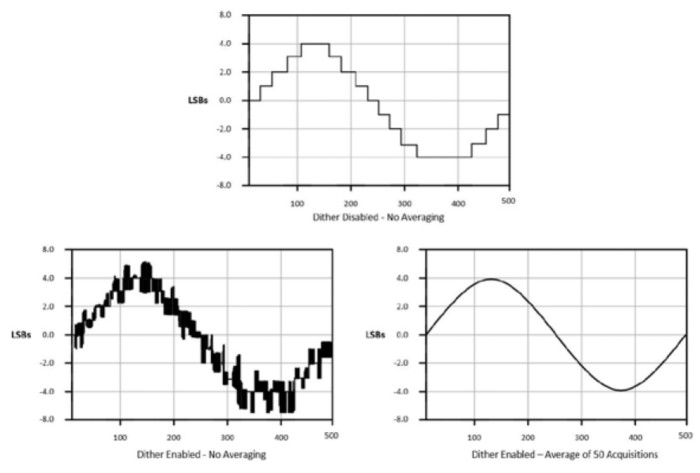
Einige Oszilloskope verwenden eine Methode mit der Bezeichnung „Dithering“ zur Glättung von Signalen, um den Eindruck einer höheren Auflösung zu vermitteln. Beim Dithering wird dem Eingangssignal absichtlich Rauschen hinzugefügt. Dadurch werden die kleinen Unterschiede in der Amplitudenauflösung verwischt. Es ist dabei wichtig, zufälliges Rauschen so hinzuzufügen, dass das Signal zwischen aufeinanderfolgenden Pegeln hin- und herspringt. Dadurch wird das Signal selbst verrauschter. Es wird jedoch geglättet, indem dieses Rauschen nach der Erfassung digital gemittelt wird.

^{Abbildung 10: Mithilfe von Dithering kann ein Signal geglättet werden.}

• Die Bandbreite beschreibt den Frequenzbereich, den ein Oszilloskop genau messen kann. Sie wird als die Frequenz definiert, bei der ein sinusförmiges Eingangssignal auf 70,7 Prozent seiner ursprünglichen Amplitude gedämpft wird, was auch als „-3 dB“-Punkt bezeichnet wird.
• Die Bandbreite ist die Differenz zwischen den Eckfrequenzen.
• Der Amplitudenfehler ist ein Prozentsatz, der das Verhältnis der Bandbreite zu den Eingangssignalfrequenzen angibt, die bei der Bestimmung des Rauschens in einem System hilfreich sind.
• Es wird empfohlen, dass die Bandbreite Ihres Oszilloskops das Drei- bis Fünffache des höchsten zu untersuchenden Frequenzanteils des gemessenen Signals beträgt, um das Signal mit minimalem Amplitudenfehler zu erfassen.
• Die Anstiegszeit eines Eingangssignals ist die Zeit, in der ein Signal von 10 Prozent auf 90 Prozent der maximalen Signalamplitude übergeht.
• Es wird empfohlen, dass die Anstiegszeit des Oszilloskops ein Drittel bis ein Fünftel der Anstiegszeit des gemessenen Signals beträgt, um das Signal mit minimalem Anstiegszeitfehler zu erfassen.
• Die Sample-Rate ist die Frequenz, mit der der A/D-Wandler den analogen Eingangssignalverlauf in digitale Daten umwandelt.
• Die Sample-Rate sollte mindestens zweimal so hoch wie die höchste zu untersuchende Frequenz im Signal sein. Normalerweise sollte sie sogar etwa fünfmal so hoch sein.
• Beim Aliasing treten in den abgetasteten Daten falsche Frequenzanteile auf.
• Die Bit-Auflösung gibt an, wie viele vertikale Pegel ein Oszilloskop zur Darstellung eines Signals verwenden kann.
• Je höher die Auflösung eines Geräts, desto höher die Genauigkeit.

• Alle Inhalte zu Messgerätegrundlagen herunterladen